Welche Mathematischen Operationen werden dabei durchgeführt?

Question

Aufgabe:

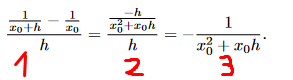
Hallo Mathelounge, ich habe Probleme nachzuvollziehen wie man von der 1. Gleichung auf die 2. Kommt und der 2. auf die 3..

Problem/Ansatz:

Welche Mathematischen Operationen werden dabei durchgeführt? Wie muss ich bei einem dreifachbruch vorgehen?

Wieso fallen soviele "h" weg vom schritt 2 auf 3.

Ich wäre sehr dankbar für eine Erklärung.

Text erkannt:

\( \frac{\frac{1}{x_{0}+h}-\frac{1}{x_{0}}}{1^{h}}=\frac{\frac{-h}{x_{0}^{2}+x_{0} h}}{2}=-\frac{1}{x_{0}^{2}+x_{0} h} \)

Answer 1

Hallo,

von 1 zu 2, betrachte nur den Zähler:

\(\frac{1}{x_0+h}-\frac{1}{x_0}\\ \text{Hauptnenner =}(x_0+h)\cdot x_0\\ \frac{ x_0}{(x_0+h)\cdot x_0}-\frac{(x_0+h)}{(x_0+h)\cdot x_0}=\frac{x_0-(x_0+h)}{(x_0+h)\cdot x_0}=\frac{-h}{(x_0+h)\cdot x_0}=\frac{-h}{x_0^2+x_0h}\)

Der ganze Bruch wird dann durch h gekürzt.

\(\displaystyle \frac{\frac{-h}{x_0^2+x_0h}}{h}=\frac{-1}{x_0^2+x_0h}\)

Gruß, Silvia

Answer 2

Im Zähler wurde der Hauptnenner gebildet.

Dabei wurden Zwischenschritte weggelassen.