Ich habe eigentlich keine konkrete Aufgabe, bräuchte aber trotzdem dringend Hilfe.
Und zwar haben wir gerade in Statistik Schätzverfahren auf dem Plan und hier schlagen meine schlechten Mathe-Kenntnisse mal wieder voll zu.
Wenn ich z.B. für die Berechnung nach der Maximum-Likelihood-Methode mit solchen Dingern konfrontiert werde:
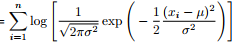
Text erkannt:
\( =\sum \limits_{i=1}^{n} \log \left[\frac{1}{\sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{1}{2} \frac{\left(x_{i}-\mu\right)^{2}}{\sigma^{2}}\right)\right] \)
Oder
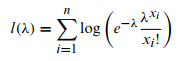
Text erkannt:
\( l(\lambda)=\sum \limits_{i=1}^{n} \log \left(e^{-\lambda} \frac{\lambda^{x_{i}}}{x_{i} !}\right) \)
Dann muss man ja zu aller erst immer die Formel erst vereinfachen und dann ableiten.
Mein Problem ist dabei vor allem erst einmal das vereinfachen. Wenn ich mir dann die Lösungsschritte anschaue, kann ich die einzelnen Schritte zu Vereinfachung zwar nachvollziehen aber das Problem ist eben: Selbst drauf gekommen wäre ich nie.
Gibt es da nicht evtl. ein "Rezept", welches man als Orientierung nehmen kann?
Oder irgendwelche anderen Tipps & Tricks wie man beim Vereinfachen vorgehen sollte?
Ich finde leider auch nicht viele Übungsaufgaben zu dem Thema (kennt ihr da vielleicht welche?). Wenn ich nach
"Übungsaufgaben Gleichungen vereinfachen" suche, dann finde ich eigentlich nur "einfachere" Aufgaben, die dann selbst ich hinbekomme. Aber leider eben nichts "komplizierteres" mit all den schönen Dingen wie Summen und Logarithmen..
Bin für jede Hilfe, Tipps und Übungsaufgaben dankbar, die Ihr mir liefern könntet! :)