Berechne das maximale Volumen einer Kiste mit Deckel mit der Länge 30cm und Breite 20cm.

Question

Aufgabe:

Berechne das maximale Volumen einer Kiste mit Deckel mit der Länge 30cm und Breite 20cm.

Problem/Ansatz:

Kann mir das bitte einer mit Rechenweg erklären und die Formel aufstellen?

Text erkannt:

Mathematik
14. 11. 23
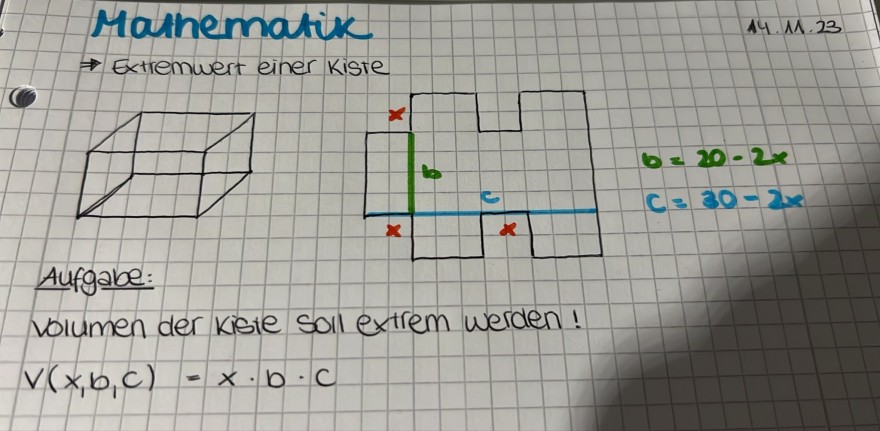
\( \Rightarrow \) Extremwert einer Kiste
\( \begin{array}{l} b=20-2 x \\ c=30-2 x \end{array} \)

Aufgabe:
volumen der kiste soll extrem werden!
\( v(x, b, c)=x \cdot b \cdot c \)

Text erkannt:

Mathematik
14. 11. 23
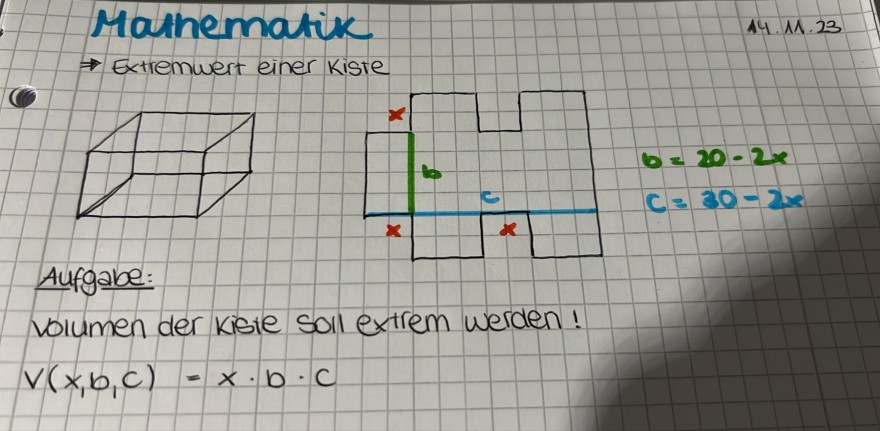
\( \Rightarrow \) Extremwert einer Kiste
\( \begin{array}{l} b=20-2 x \\ c=30-2 x \end{array} \)

Aufgabe:
volumen der kiste soll extrem werden!
\( v(x, b, c)=x \cdot b \cdot c \)

Answer 1

f(x) = x(20-2x)(30-2x)

Berechne: f '(x) = 0

Comments

Auch wenn die Kiste einen Deckel hat? So hatten wir es nämlich nur bei der ohne Deckel berechnet

---

Beim Volumen spielt der Deckel keine Rolle.

Grundfäche und Deckelfläche sind gleich, auch wenn der Deckel fehlt.

Nur bei der Oberflächenmaximierung wäre er von Bedeutung.