Volumen einer Kugel durch Volumenintegral bestimmen

Question

Aufgabe:

Volumen einer Kugel durch Volumenintegral bestimmen

Problem/Ansatz:

Hallöchen,

Die Formel für das Volumen ist ja$$\frac{4}{3}πr^{3}$$ Ich soll jetzt aber mithilfe eines Volumenintegrals diese Formel herleiten und weiß nicht, mit welchen Grenzen bzw. Funktionen ich die Integrale durchführen muss. Die genaue Fragestellung lautet:

Leiten Sie das Volumen einer Kugel mit Radius R her. Gehen Sie dabei wie folgt vor:
1) Wählen Sie zuerst entsprechend der Symmetrie der Kugel ein Koordinatensystem.
2) Schreiben Sie das Integral auf und legen Sie die Grenzen fest.
3) Führen Sie die Integration aus.

Das integrieren ist eher weniger das Problem sondern lediglich das Verständnis wie ich anfange. Danke im Voraus!

Comments

https://www.youtube.com/watch?v=-lyFG-w_B0E

Answer 1

Rotation um die x-Achse (allgemein für Volumen):

\(V= π \cdot \int\limits_{a}^{b}(f(x))^{2}dx \)

Ich würde die Grenzen bei \(a=0\)  und \(b=r\)  wählen, da Symmetrie

\(V= 2 \cdot π \cdot \int\limits_{0}^{r}(r^2-x^2)dx \)

\(V= 2 \cdot π \cdot \int\limits_{0}^{r}(r^2-x^2)dx =2 \cdot π[r^2*x-\frac{1}{3}x^3]_{0}^{r}\\=2 \cdot π[r^2*r-\frac{1}{3}r^3]-[2 \cdot π\cdot 0]\\=2 \cdot π[r^3-\frac{1}{3}r^3]\\=2 \cdot π[\frac{2}{3}r^3]\\= \frac{4}{3}r^3 \cdot π \)

Answer 2

Tipp: Verwende Polarkoordinaten/Kugelkoordinaten.

Answer 3

Hallo,

Willkommen in der Mathelounge!

Ich verwende im Folgenden Kugelkoordinaten \(\varphi\), \(\theta\) und \(r\), wie sie hier beschrieben sind.

Ich betrachte zunächst nur ein Achtel der Kugel, also dass was sich in einem kartesichen Koordinatensystem in einem der 8 Quadranten befindet, wenn der Kugelmittelpunkt im Ursprung liegt.

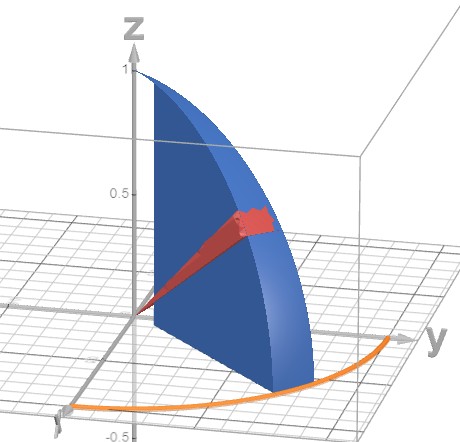
Dort schneide ich ein senkrechtes Kuchenstück heraus (blau) und daraus einen kleinen Kegel (rot) dessen Spitze sich im Ursprung des KS befindet. Das Volumen des roten Kegels ist bekanntermaßen $$V_{\text{Kegel}} = \frac{1}{3}r G $$wenn \(G\) die Grundfläche ist.

Und die Grundfläche \(G\) kann man ansetzen als $$G=r\sin(\theta)\text{d}\theta\,r\text{d}\varphi$$ Kannst Du nun das Integral aufstellen? Falls nicht, findest Du den Lösungsweg hinter dem Spoiler

[spoiler]

$$\begin{aligned} V_{\text{Kugel}} &=8\int\limits_{\varphi=0}^{\pi/2} \int\limits_{\theta=0}^{\pi/2} \frac{1}{3}r \cdot \underbrace{r\sin(\theta)\text{d}\theta\,r\text{d}\varphi}_{=G}\\ &= \frac{8r^3}{3}\int\limits_{\varphi=0}^{\pi/2}\underbrace{\left[-\cos(\theta)\right]_{\theta=0}^{\pi/2}}_{=1}\,\text{d}\varphi \\ &= \frac{8r^3}{3} \left[\frac{\pi}{2} - 0\right] \\ &= \frac{4}{3}\pi r^3\\ \end{aligned}$$

[/spoiler]

Gruß Werner