Goldener Schnitt herleiten

Question

Zeigen sie, dass gilt φ^2 = φ+1 beim goldenen Schnitt, wenn gilt φ := |AB| : |AC| = |AC| : |CB|.

und folgern sie daraus: φ=\( \frac{1+\sqrt{5}}{2} \)

Comments

Und zu diesem Klassiker hast du absolut gar nichts im Internet gefunden?

Was hast du denn schon?

Answer 1

Ich nehme an dazu gehört diese Skizze

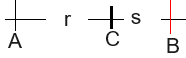
Dann ist \( \frac{r+s}{r} \)=\( \frac{r}{s} \) oder 1+\( \frac{s}{r} \)=\( \frac{r}{s} \).

Für \( \frac{r}{s} \) =x ist \( \frac{s}{r} \) =\( \frac{1}{x} \) und folglich

1+\( \frac{1}{x} \)=x oder x+1=x². Das ist eine quadratische Gleichung mit der positiven Lösung \( \frac{1+\sqrt{5}}{2} \).

Comments

diese Skizze gehört dazu

---

Sag ich doch!

---

Wurzel aus 5!