Hallo,
stelle bitte demnächst deine Fragen einzeln ein.
Eine Funktion 3. Grades und ihre ersten beiden Ableitungen kann man schreiben als
\(f(x)=ax^3+bx^2+cx+d\\ f'(x)=3ax^2+2bx+c\\ f''(x)=3ax+2b\)
Du brauchst vier Gleichungen für die vier Unbekannten.
\(\text{Punkt }(1\mid6,75)\Rightarrow f(1)=6,75\\ 1. \quad a+b+c+d=6,75\\ \text{Steigung 2,25}\Rightarrow f'(1)=2,25\\ 2.\quad 3a+2b+c=2,25\\ \text{Extrempunkt bei }(4\mid0)\Rightarrow f(4)=0\quad f'(4)=0\\ 3.\quad 64a+16b+4c+d=0\\ 4.\quad 48a+8b+c=0\)
Lösung s. Aufgabe b).
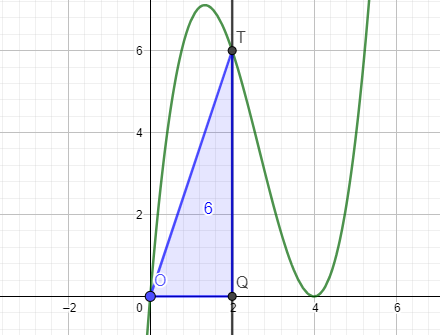
Flächeninhalt des Dreiecks:
\(A=\frac{u\cdot f(u)}{2}=\frac{u\cdot (\frac{3}{4}u^3-6u^2+12u)}{2}=\frac{\frac{3}{4}u^4-6u^3+12u^2}{2}=\frac{3}{8}u^4-3u^3+6u^2\)
Bilde die 1. Ableitung A', setze sie = 0 und löse nach u auf.
[spoiler]
\(\frac{3}{2}u^3-9u^2+12u=0\\ \frac{3}{2}u\cdot(u^2-6u+8)=0\\ u_1=0\quad \vee \\ u^2-6u+8=0\\ u_{2,3}=3\pm\sqrt{9-8}=0\\ \green {u_2=2}\quad u_3=4 \)
[/spoiler]
Gruß, Silvia