Berechne die Eckpunkte des Rechteckes so, dass der Flächeninhalt des Rechteckes maximal wird.

Question

Gegeben ist die Funktion \( f \) mit \( f(x)=\frac{1}{9} x^{4}-2 x^{2}+9 \)
a) Untersuche die Funktion vollständig (ohne Skizze).

Der Graph der Funktion schließt mit der \( \mathrm{x} \)-Achse eine Fläche ein. In diese Fläche soll ein symmetrisches Rechteck gelegt werden.
b) Skizziere den Sachverhalt in der gegebenen Skizze und benenne die Punkte.
c) Berechne die Eckpunkte des Rechteckes so, dass der Flächeninhalt des Rechteckes maximal wird.

Comments

Hallo,

\( \max \left\{\frac{x^{5}}{9}-2 x^{3}+9 x\right\}=\frac{432}{25 \sqrt{5}} \) at \( x=\frac{3}{\sqrt{5}} \)

 :-)

Answer 1

A(x) = x*f(x)

Berechne: A'(x) = 0

Answer 2

b)

c) A(u)=2u·f(u)=2u·(\( \frac{u^4}{9} \)-2u²+9).

Erste Ableitung Null setzen; ergibt u=3.

Comments

Es gibt 2 Lösungen:

https://www.wolframalpha.com/input?i=maximize+%281%2F9*x%5E4-2x%5E2%2B9%29*x

---

Die Funktion ist falsch.

Die zweite Lösung erübrigt sich, wenn man vorher den Definitionsbereich festlegt, was man bei derartigen Aufgaben sowieso machen sollte.

---

Schreibfehler wurde korrigiert.

Answer 3

Hallo,

Nullstellen, Extrema und Wendepunkte s. Graph der Funktion:

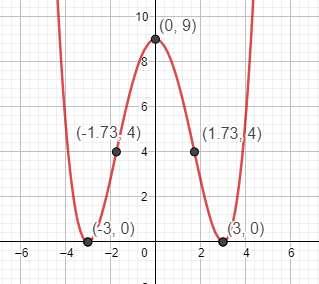
b)

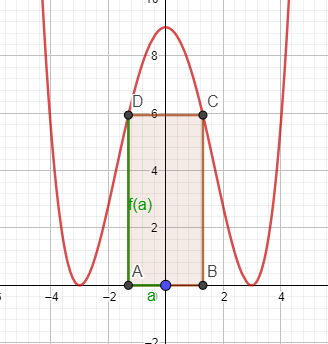
c) Flächeninhalt des Rechtecks:

\(A=2a\cdot f(a)=2a\cdot\bigg( \frac{1}{9}a^4-2a^2+9\bigg)=\frac{2}{9}a^5-4a^3+18a\\ \)

Bilde die 1. Ableitung, setze sie = 0 und löse nach a auf:

\(A=2a\cdot f(a)=2a\cdot\bigg( \frac{1}{9}a^4-2a^2+9\bigg)=\frac{2}{9}a^5-4a^3+18a\\ \frac{10}{9}a^4-12a^2+18=0\\
a=1,34\)

Gruß, Silvia