Bestimmung des Widerstands R durch Minimierung des quadratischen Fehlers

Question

Bekanntlich gilt das physikalische Gesetz \( U=R I \). Messungen haben die folgenden Werte \( U_{i} \) und \( I_{i} \) für \( i= \) \( 1,2,3,4 \) ergeben:

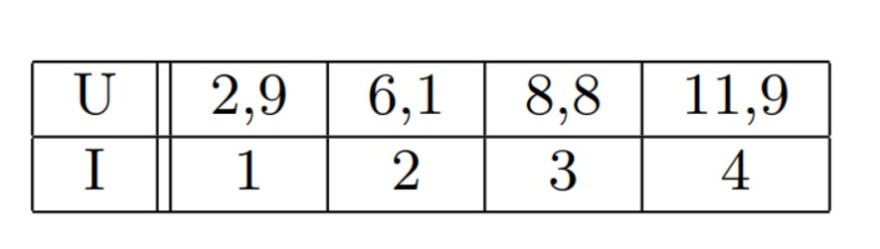
\( U=R I \) passt also nicht perfekt. Nutzen Sie Theorem 3.7 aus der Vorlesung, um \( R \) so zu bestimmen, dass der quadratische Fehler \( \sum \limits_{i=1}^{4}\left(U_{i}-R I_{i}\right)^{2} \) minimal wird.

Theorem 3.7
Sei \( U \) ein Unterraum von \( V \) und \( w \in V \). Wenn \( \hat{w} \in U \) und \( w-\hat{w} \perp U \), dann gilt \( \|w-\hat{w}\|<\|w-u\| \quad \forall u \in U \backslash\{\hat{w}\} \).

Answer 1

Im Sinne der Aufgabe ist meines Erachtens wie folgt vorzugehen.

Wir haben die Vektoren

$$u=(U_i), i = (I_i)$$

Es ist die orthogonale Projektion von \(u \) auf den von \(i\) aufgespannten Unterraum gesucht:

$$R=\frac{u\cdot i}{|i|^2}= \frac{2.9\cdot 1 + 6.1\cdot 2 + 8.8\cdot 3 + 11.9\cdot 4}{1^2+2^2+3^2+4^2}=2.97$$

Damit ist \(\boxed{Ri}\) die Bestapproximation von \(u\) im Sinne von Theorem 3.7.

Answer 2

Hallo

was der Satz hilft weiss ich nicht, aber die Summe nach r ableiten und 0 setzen gibt das Minimum

Gruß lul

Answer 3

Das Theorem liefert, dass \(||U-RI||\) minimal ist, und damit auch \(||U-RI||^2\)), wenn \(U-RI\) senkrecht auf \(RI\) steht, also für das Skalarprodukt \(\langle U-RI, RI\rangle=0\) gilt.

Die Rechnung mit der Ableitung geht aber wesentlich schneller.

Answer 4

[1; 2; 3; 4]^T·([1; 2; 3; 4]·x - [2.9; 6.1; 8.8; 11.9]) = 0

aufgelöst nach x ergibt

x = ([1; 2; 3; 4]^T·[2.9; 6.1; 8.8; 11.9]) / ([1; 2; 3; 4]^T·[1; 2; 3; 4]) = 2.97