Which of the following maps are linear?

Question

Aufgabe: Linear Mapping and matrix

Text erkannt:

Which of the following maps are linear?
\( \begin{array}{l} \vee \mathbb{R}^{2} \rightarrow \mathbb{R} \text { with }\left(\begin{array}{l} x_{1} \\ x_{2} \end{array}\right) \mapsto\left(x_{1} \cdot x_{2}\right) \\ \vee \mathbb{R}^{2} \rightarrow \mathbb{R}^{2} \text { with }\left(\begin{array}{l} x_{1} \\ x_{2} \end{array}\right) \mapsto\left(\begin{array}{c} x_{1} \cdot x_{2} \\ x_{1}+x_{2} \end{array}\right) \\ \vee \mathbb{R}^{2} \rightarrow \mathbb{R}^{2} \text { with }\left(\begin{array}{l} x_{1} \\ x_{2} \end{array}\right) \mapsto\left(\begin{array}{l} -1 x_{1}-1 x_{2} \\ -2 x_{1}+2 x_{2} \end{array}\right) \end{array} \)

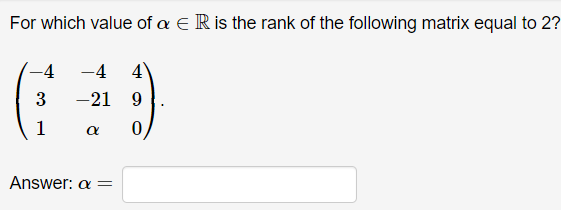
Text erkannt:

For which value of \( \alpha \in \mathbb{R} \) is the rank of the following matrix equal to 2 ?
\( \left(\begin{array}{ccc} -4 & -4 & 4 \\ 3 & -21 & 9 \\ 1 & \alpha & 0 \end{array}\right) \)

Answer: \( \alpha= \)

Problem/Ansatz: kann mir hier einer helfen, ich habe viele Rechnung gemacht aber die Lösung sind immer wieder falsch?

Answer 1

1 und 2 sind nicht linear. 3 allerdings schon.

weil bei \(  \left(\begin{array}{l} x_{1} \\ x_{2} \end{array}\right) \mapsto\left(x_{1} \cdot x_{2}\right)   \)   hat man z.B.

\(  \left(\begin{array}{l} 1+3 \\ 1+4 \end{array}\right) \mapsto\left(4 \cdot 5\right) = 20\)

Aber \(  \left(\begin{array}{l} 1\\ 1 \end{array}\right) \mapsto\left(1 \cdot 1\right) = 1   \)

und \(  \left(\begin{array}{l} 3\\ 4 \end{array}\right) \mapsto\left(3 \cdot 4\right) = 12  \)

Aber  1+12 ≠20.      etc.

Comments

Dankee weißt du auch wie man die andere Aufgabe löst?

---

Die Determinante ist 48(α+1). Also ist sie 0 für α=1

Dann ist jedenfalls der Rang kleiner als 3.

Da die 1 und 2. Zeile offenbar keine Vielfachen

voneinander sind, ist der Rang jedenfalls ≥ 2.

Also für α=1 ist er gleich 2.

---

Das hat leider nicht geklappt, aber trotzdem danke :)

---

Hatte mich ja vertan. Muss -1 sein.