Consider a linear time series model of the following form

Question

Aufgabe:

Consider a linear time series model of the form

\( y_{t}=\rho y_{t-1}+\varepsilon_{t}, \quad t=1, \ldots, T \)
with \( \varepsilon \sim \mathcal{N}\left(0, \sigma^{2} I_{N}\right) \) and \( \rho<1 \). Let \( \hat{\rho} \) be the OLS estimator of \( \rho \).

(a) Is \( \hat{\rho} \) unbiased?
(b) Is \( \hat{\rho} \) consistent?
(c) Are ED1-3 fulfilled?

Problem/Ansatz:

Bräuchte dringend Hilfe bei folgender Aufgabe....

Comments

WzT ist ED1-3 ??

---

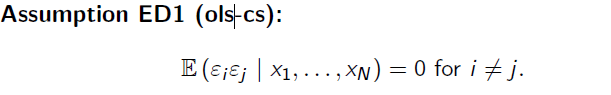
Text erkannt:

Assumption ED1 (ols-cs):
\( \mathbb{E}\left(\varepsilon_{i} \varepsilon_{j} \mid x_{1}, \ldots, x_{N}\right)=0 \text { for } i \neq j \)

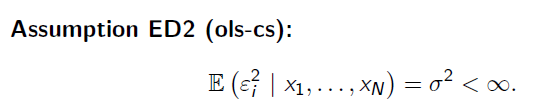
Text erkannt:

Assumption ED2 (ols-cs):
\( \mathbb{E}\left(\varepsilon_{i}^{2} \mid x_{1}, \ldots, x_{N}\right)=\sigma^{2}<\infty \)

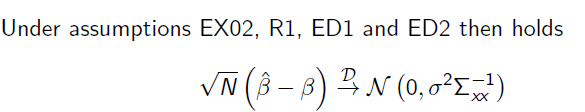
Text erkannt:

Under assumptions EX02, R1, ED1 and ED2 then holds
\( \sqrt{N}(\hat{\beta}-\beta) \stackrel{\mathcal{D}}{\rightarrow} \mathcal{N}\left(0, \sigma^{2} \Sigma_{x x}^{-1}\right) \)