Aufgabe: Die Gewinnentwicklung in Euro pro Woche beim Verkauf eines neuen Produktes wird in den ersten 12 Monaten mit der Funktion f(x)=-20x^3+240x^2-1200 beschrieben (siehe Diagramm). Die Zahlen auf der Zeitachse geben jeweils das Ende des Monats an. Ermitteln Sie den Gesamtgewinn in den ersten 4 Monaten und vom Beginn des 2. Monats bis zum Ende des 10. Monats. Ermitteln Sie ebenfalls den Gesamtverlust.
Problem: Ich habe die jeweiligen Gesamtgewinne raus, also -960 Euro bei den 4 Monaten und 1925 Euro bei 2-10. Aber ich weiß nicht, wie ich den Gesamtverlust berechnen soll. Die Graphik habe selbt noch einmal gezeichnet und die Stammfunktion auch noch mal dazu gezeichnet.
b) \( \begin{array}{l} \int \limits_{0}^{4}-20 x^{3}+240 x^{2}-1200 d x=\left[-5 x^{4}+80 x^{3}-1200 x\right]_{0}^{4} F(4)-F(0) \\ \left(5 \cdot 4^{4}+80 \cdot 4^{3}-1200 \cdot 4\right)-0=-960 \epsilon \\ \int \limits_{1}^{10}-20 x^{3}+240 x-1200 d x=\left[-5 x^{4}+80 x^{3}+1200 x\right]_{2}^{10} F(10)-F(1) \\ \left(5 \cdot 10^{4}+80 \cdot 10^{3}-1200 \cdot 10\right)-\left(5 \cdot 1^{4}+80.1^{3}-1200 \cdot 1\right)=19.125 \epsilon\end{array} \)
Text erkannt:
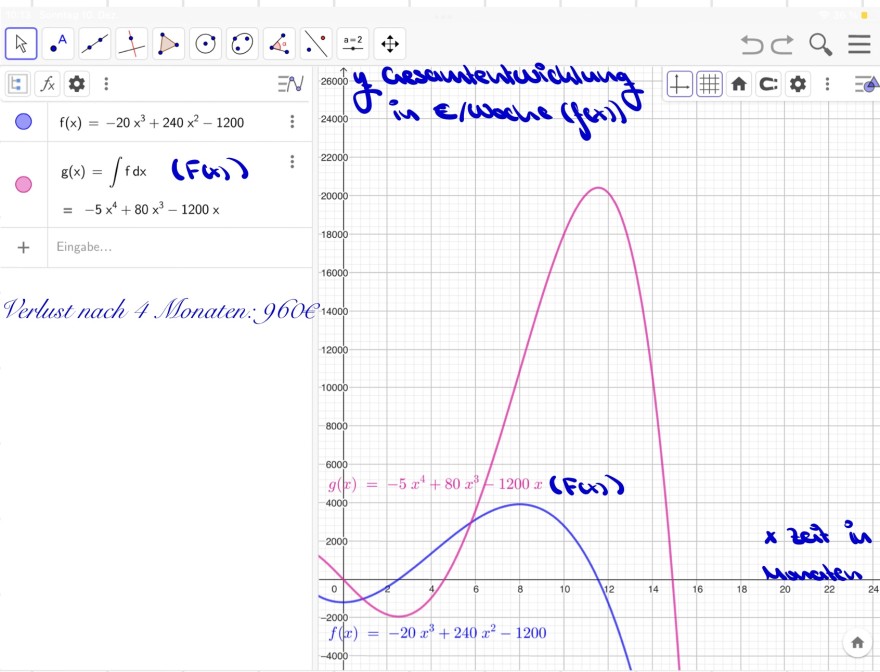
\( f(x)=-20 x^{3}+240 x^{2}-1200 \) in \( / \) wache \( (f(x) \) )
\( \mathrm{g}(\mathrm{x})=\int \mathrm{fdx}(\boldsymbol{F}(\mathrm{x})) \)
\( =-5 x^{4}+80 x^{3}-1200 x \)
Terlust nach 4. Monaten: 9606