Aufgabe: Auflösen des Gleichungssystems
Problem/Ansatz:
Hallo, ich versuche dieses Gleichungssystem in der Matrix-Schreibweise zu lösen allerdings komme ich ständig auf das falsche Ergebnis..
Wie mein Ansatz bis jetzt war: 1. 2x2 Matrix invertieren, 2. Determinante in Matrix ziehen und 2x2 mit 2x1 Matrix multiplizieren, danach auflösen nach x1 und den wert wiederum einsetzten..
Vergesse ich hier was oder passt etwas nicht in meinem Ansatz?
Vielen Danke schon mal :)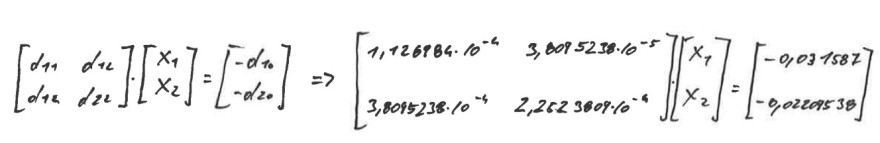
Text erkannt:
\( \left[\begin{array}{ll}d_{11} & d_{12} \\ d_{12} & d_{22}\end{array}\right] \cdot\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right]=\left[\begin{array}{l}-d_{10} \\ -d_{20}\end{array}\right] \Rightarrow\left[\begin{array}{ll}1,126884 \cdot 10^{-4} & 3,0085238 \cdot 10^{-5} \\ 3,8095238 \cdot 10^{-4} & 2,2623809 \cdot 10^{-4}\end{array}\right]\left[\begin{array}{l}x_{1} \\ x_{2}\end{array}\right]=\left[\begin{array}{l}-0,031582 \\ -0,02205538\end{array}\right] \)