Bestimmen Sie, wie groß der Parameter k mindestens sein muss, damit Folgendes gilt:

Question

Aufgabe:

Die Zufallsgröße X ist binomialverteilt mit n=60 und D=0.20. Bestimmen Sie, wie groß der Parameter k mindestens sein muss, damit Folgendes gilt:

a) P(X≤ k) ≥0,5

b) P(X≤ k) ≥0,8

c P(X≥k)≤  0,2

d P(X ≥ k)≤ 0,4

Problem/Ansatz:

Wie rechne ich hier k aus?

Comments

Was ist D in diesem Zusammenhang?

---

Vermutlich \(p\). Alles andere ergibt ja auch keinen Sinn.

Answer 1

Wenn man keine Tabelle der Kumulierten Binomialverteilung für n = 60 hat, dann kann man

1. einen Rechner wie Geogebra nutzen.

a) P(X ≤ k) ≥ 0,5

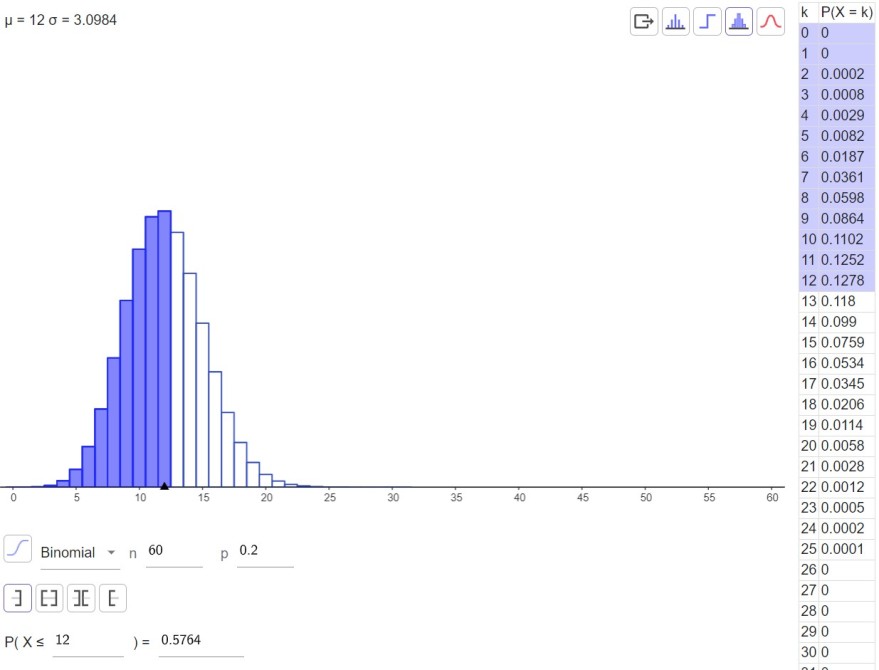
2. eine erste Näherung mit der Normalverteilung bestimmen und dann mit der Binomialverteilung nach optimieren.

μ = n·p = 12 ; σ = √(n·p·q) = 3.0984

a) P(X ≤ k) = NORMAL((k + 0.5 - 12)/3.0984) = 0.5 --> k = 11.5

Hier würde man also als erstes k = 12 probieren und liegt damit auch schon richtig, was man bei einem Test mit der kumulierten Binomialverteilung sehen würde.

Answer 2

Passenden Wert aus der Tabelle heraussuchen, mit dem Taschenrechner und der entsprechenden Funktion dich an den Wert herantasten. Es gibt auch bei einigen Taschenrechnern die Funktion InvB, womit man \(k\) für \(P(X\leq k)\leq \alpha\) berechnen kann.

Answer 3

Hier ein Tool , mit dem du dich rantasten kannst. Es geht nur durch Probieren oder mit Tabellenwerk.

https://www.arndt-bruenner.de/mathe/scripts/normalverteilung1.htm

a) k= 12

b) k=9

c) k= 8

d) k= 10