Aufgabe:
Hungrige Mäuse tummeln sich vor dem Eingang A(0I4) eines Labyrinths. Zufallsgeneratoren an jeder der 12 „Kreuzungen“ des Labyrinths (also z.B. im Punkt (0I2), aber nicht im Punkt (2I0)) öffnen jeder Maus genau einen kürzesten Weg von A zum Futterplatz Z (3I0). Die Öffnung „nach rechts“ erfolgt dabei jeweils mit einer Wahrscheinlichkeit von 0,4 und die „nach unten“ mit einer Wahrscheinlichkeit von 0,6.
Ermitteln Sie bei jedem der vier kürzesten Wege 1 bis 4 die Wahrscheinlichkeit, dass die Maus ihn nimmt.
Ansatz:
Bernoulli Ketten
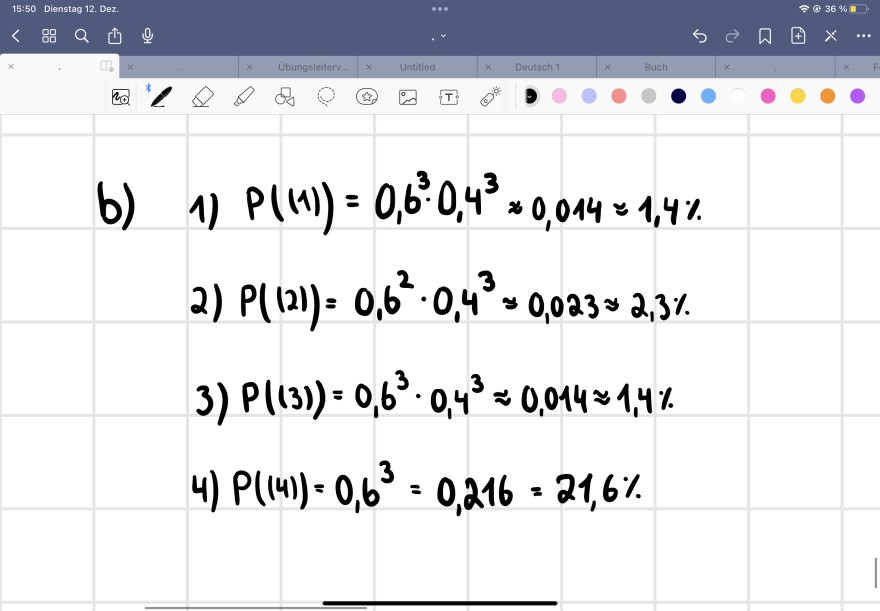
Text erkannt:
(1)(2)(3)(4)
Sorry.
Ich hatte die Aufgabenstellung falsch gelesen. Dort steht ja klar das die Zufallsgeneratoren nur an 12 Kreuzungen sind. Eben nicht am rechten und unterem Rand.
Hier meine Verbesserung. Die Wahrscheinlichkeiten wären dann wie folgt:
(1) P(u r u r u r u) = 0.6·0.4·0.6·0.4·0.6·0.4·1 = 0.013824(2) P(r u r u r u u) = 0.4·0.6·0.4·0.6·0.4·1·1 = 0.02304(3) P(r u u u r r u) = 0.4·0.6·0.6·0.6·0.4·0.4·1 = 0.013824(4) P(u u u u r r r) = 0.6·0.6·0.6·0.6·1·1·1 = 0.1296
Da ist das Ergebnis bei allen vier Wegen gleich. Ist die Bernoulli zu beginn dann 7 von 7?
Es ist korrekt, dass du für alle 4 Pfade die gleiche Wahrscheinlichkeit bekommst.
Beachte: Der Binomialkoeffizient wird nur benutzt, wenn es um die Berechnung mehrerer Pfade gilt.
Es könnte durchaus in einer Folgeaufgabe gefragt sein, wie viele solcher kürzesten Pfade es gibt.
Beachte das Wegenetz für die Maus nicht vollständig ist. Sie könnte der Aufgabe nach ja auch 7 mal nach rechts gehen oder 7 mal nach unten gehen. Beides führt die Maus nicht ins Ziel.
Die Aufgabe ist dahingehend also missverständlich gestellt.
Danke :)
Das ist sogar eine Aufgabe haha
Mir war nicht klar dass man das berechnen kann. Wäre es möglich mir dabei zu helfen?
Ein kürzester Weg besteht aus 7 Schritten, wobei genau 4 nach unten und 3 nach rechts gegangen werden müssen.
Ein Weg wäre also: u r u r u r u
Wie viele Wege es jetzt gibt, kann man jetzt z.B. mit dem Binomialkoeffizienten leicht ermitteln.
Wie genau kann man das mit einem Binominalkoeffizient lösen?
Quatsch.
Wie ist es dann richtig?
Die vier Pfade haben drei verschiedene Wahrscheinlichkeiten.
b) 1) \( P((1))=0,6^{3} \cdot 0,4^{3} \times 0,014=1,4 \% \)2) \( P(12)=0,6^{2} \cdot 0,4^{3} \approx 0,023 \approx 2,3 \% \)3) \( P((3))=0,6^{3} \cdot 0,4^{3} \approx 0,014 \approx 1,4 \% \)4) \( P((4))=0,6^{3}=0,216=21,6 \% \)
Ist das richtig?
Und wie lässt sich die Anzahl der kürzesten Wege berechnen?
Ist das richtig?P((4)) = 0,6^4
die Anzahl der kürzesten Wege= (7 über 3)
Das kann nicht 0,6^4 sein weil bei (0|0) keine Kreuzung ist und somit die Maus automatisch nach rechts geht.
Warum 7 über 3? Also 7 verstehe ich, aber warum 3?
Ich hatte die Aufgabenstellung falsch gelesen. Dort steht ja klar, dass die Zufallsgeneratoren nur an 12 Kreuzungen sind. Eben nicht am rechten und unterem Rand.
Ich habe meine obige Antwort korrigiert.
Ein anderes Problem?
Willkommen bei der Mathelounge! Stell deine Frage einfach und kostenlos
