Aufgabe:
Wie löse ich die Gleichung nach ( r)?
User
8659=2000/r *[ 1- (1/(1+r)^10)]
Problem/Ansatz:
Hier Tipp wenn du möchtest
Text erkannt:
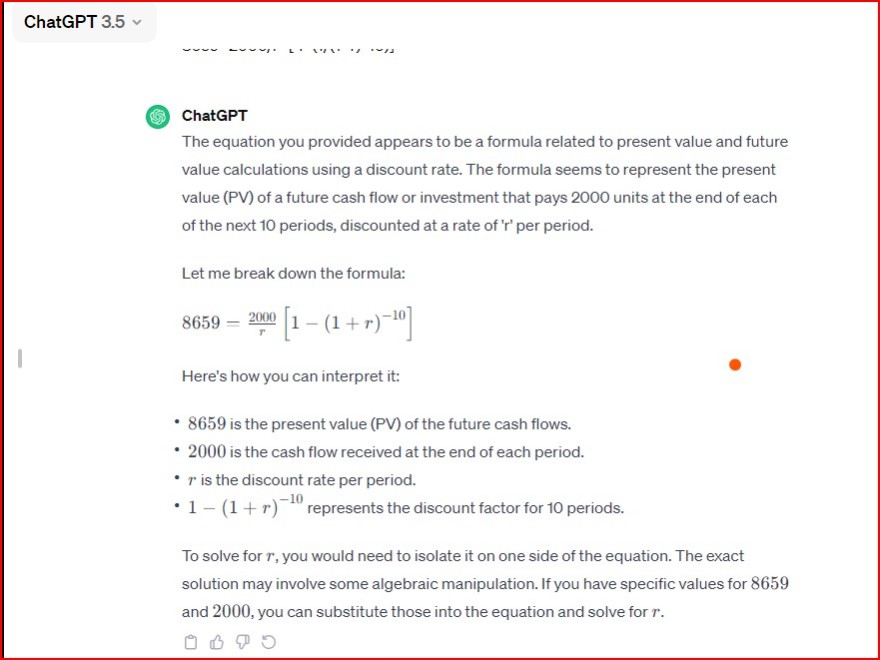
ChatGPT 3.5
ChatGPT
The equation you provided appears to be a formula related to present value and future value calculations using a discount rate. The formula seems to represent the present value (PV) of a future cash flow or investment that pays 2000 units at the end of each of the next 10 periods, discounted at a rate of ' \( r \) ' per period.
Let me break down the formula:
\( 8659=\frac{2000}{r}\left[1-(1+r)^{-10}\right] \)
Here's how you can interpret it:
- 8659 is the present value (PV) of the future cash flows.
- 2000 is the cash flow received at the end of each period.
- \( r \) is the discount rate per period.
- \( 1-(1+r)^{-10} \) represents the discount factor for 10 periods.
To solve for \( r \), you would need to isolate it on one side of the equation. The exact solution may involve some algebraic manipulation. If you have specific values for 8659 and 2000 , you can substitute those into the equation and solve for \( r \).