Aufgabe:
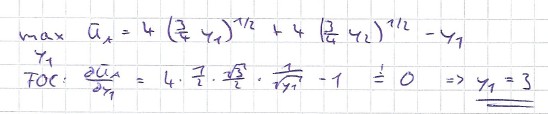
Text erkannt:
\( \begin{array}{l}\max a_{A}=4\left(\frac{3}{4} y_{1}\right)^{1 / 2}+4\left(\frac{3}{4} y_{2}\right)^{1 / 2}-y_{1} \\ \text { FOC: } \frac{\partial \bar{u}_{A}}{\partial y_{1}}=4 \cdot \frac{1}{2} \cdot \frac{\sqrt{3}}{2} \cdot \frac{1}{\sqrt{y_{1}}}-1 \Rightarrow 0 \Rightarrow y_{1}=3 \\\end{array} \)
Problem/Ansatz:
Hallo zusammen, könntet ihr mir helfen, warum man auf auf dieses Ergebniss kommt? Ich komme bei meiner Rechnung auf das Ergebniss 1,5 o. 6/4 statt 3,0. Welchen Fehler habe ich hierbei gemacht?
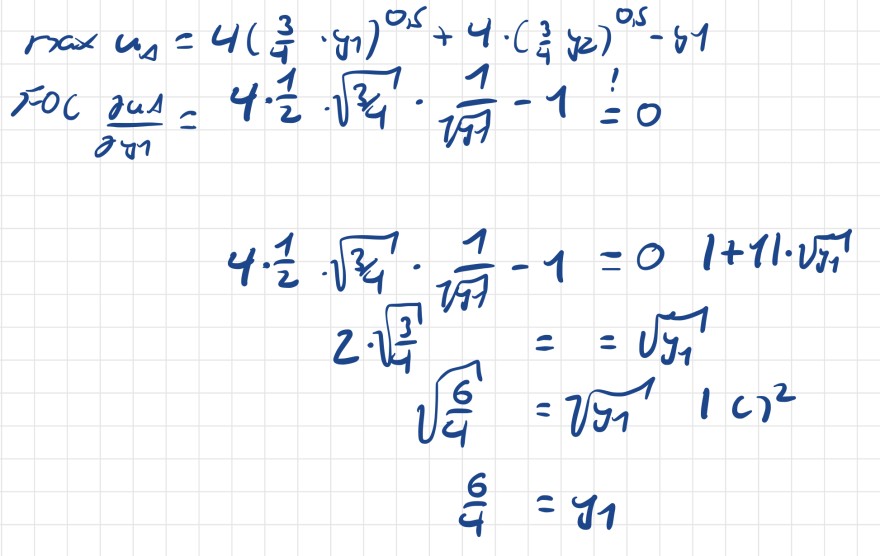
Text erkannt:
\( \begin{array}{l} \operatorname{rax} u_{\Delta}=4\left(\frac{3}{4} \cdot y_{1}\right)^{0,5}+4 \cdot\left(\frac{3}{4} y_{2}\right)^{0,5}-s_{1} \\ \operatorname{FOC} \frac{\partial u d}{\partial y_{1}}=4 \cdot \frac{1}{2} \cdot \sqrt{\frac{3}{4}} \cdot \frac{1}{\sqrt{37}}-1=0 \\ 4 \cdot \frac{1}{2} \cdot \sqrt{\frac{3}{4}} \cdot \frac{1}{\sqrt{y 1}}-1=0 \quad 1+11 \cdot \sqrt{y_{1}} \\ 2 \cdot \sqrt{\frac{3}{4}}=\sqrt{y_{1}} \\ \sqrt{\frac{6}{4}}=\sqrt{y_{1}} \quad(c)^{2} \\ \frac{6}{4}=y_{1}\end{array} \)
Text erkannt:
\( \begin{array}{l}\max a_{A}=4\left(\frac{3}{4} y_{1}\right)^{1 / 2}+4\left(\frac{3}{4} y_{2}\right)^{1 / 2}-y_{1} \\ \text { FOC: } \frac{\partial \bar{u}_{A}}{\partial y_{1}}=4 \cdot \frac{1}{2} \cdot \frac{\sqrt{3}}{2} \cdot \frac{1}{\sqrt{y_{1}}}-1 \Rightarrow 0 \Rightarrow y_{1}=3 \\\end{array} \)