Bestimmen Sie die reellen Fourier-Koeffizienten a_{5} und b_{5} der skizzierten Funktion f mit Periode T=4 .

Question

Aufgabe:

Text erkannt:

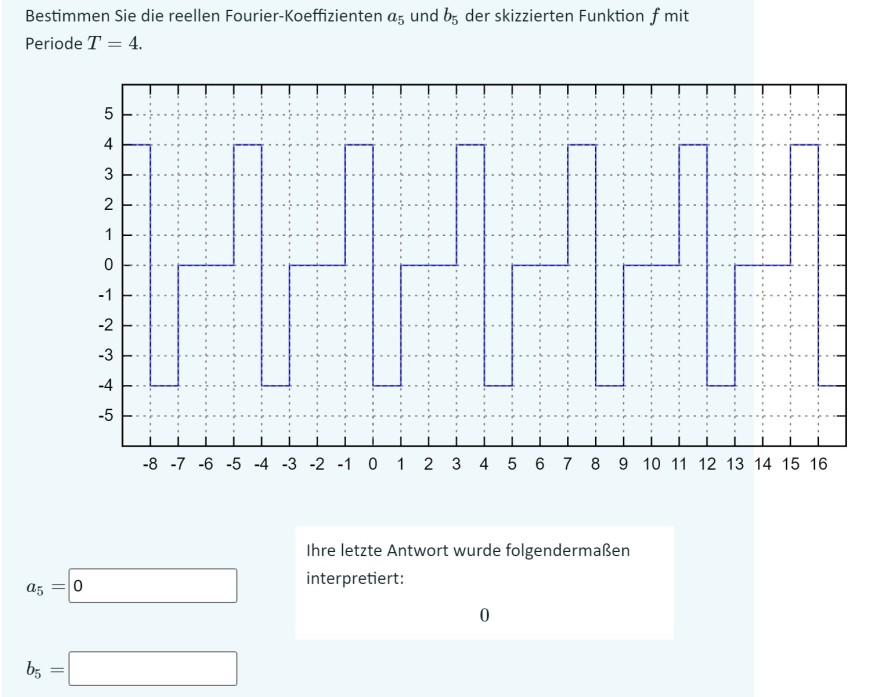
Bestimmen Sie die reellen Fourier-Koeffizienten \( a_{5} \) und \( b_{5} \) der skizzierten Funktion \( f \) mit Periode \( T=4 \).
Ihre letzte Antwort wurde folgendermaßen
\( a_{5}=0 \)
interpretiert:
0
\( b_{5}= \)

Problem/Ansatz:

Aufgrund von Symmetrie habe ich a_{5} = 0

Leider weiß ich nicht so recht wie ich auf dass Ergebnis von b_{5} kommen soll. Kann mir da jemand weiterhelfen?

Comments

Wie lautet denn die Formel zu r Berechnung von b_5?

---

Die Formel für b_5 habe ich, allerdings weiß ich nicht in welchem Intervall ich dass Integral ausrechnen muss.

---

Bei einer periodischen Funktion kann man über ein beliebiges Intervall der Länge T integrieren, z.B. über [-2,2]

---

als Stammfunktion hab ich jetzt: 8/(3*pi) *cos(((5*pi)/2) *t), aufgrund von Symmetrie habe ich die Grenzen 0 bis 2. Grenzen eingesetzt komme ich auf b_5 = 0. ist dass Korrekt?.

Answer 1

Ich komme auf \(b_5=-4\int\limits_0^1 \sin(\frac{5\pi}2t)\, dt = \frac8{5\pi}\cos (\frac{5\pi}2t)\big|_0^1 =-\frac8{5\pi}\)