Aufgabe:
Eine Kostenfunktion für ein bestimmtes Produkt ist gegeben durch C(Q)=3Q^2 +2Q+75
wobei Q die produzierte Menge bezeichnet. Bestimmen Sie die durchschnittliche Kostenfunktion AC.
Finden Sie den positiven stationären Punkt von AC und prüfen Sie, ob es sich tatsächlich um einen zumindest lokalen Minimierer handelt. Wie hoch sind die minimalen Durchschnittskosten? Welches Verhältnis besteht zwischen den Grenzkosten und den Durchschnittskosten im stationären Punkt?
Problem/Ansatz:
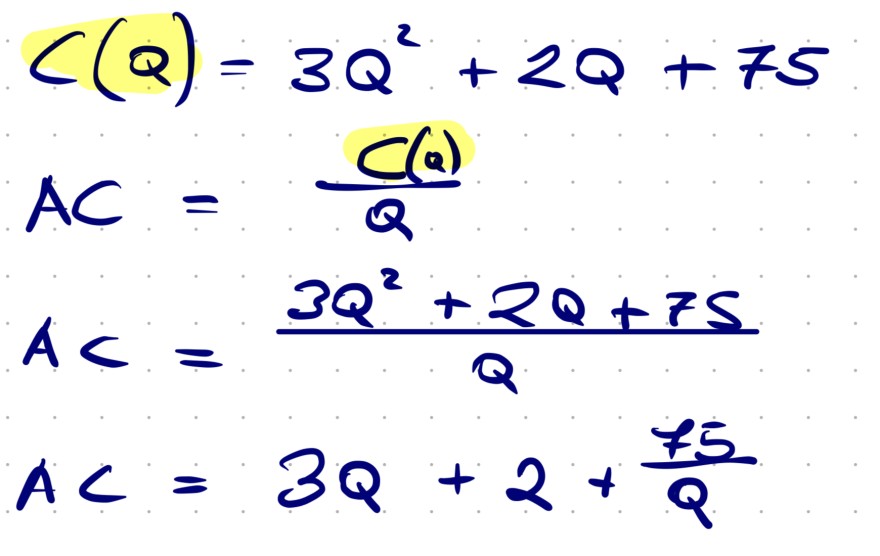
Text erkannt:
\( \begin{array}{l}C(Q)=3 Q^{2}+2 Q+75 \\ A C=\frac{C Q}{Q} \\ A C=\frac{3 Q^{2}+2 Q+75}{Q} \\ A C=3 Q+2+\frac{75}{Q}\end{array} \)
Im Moment ist das die Formel, die ich gelöst habe. Ich bin mir aber nicht sicher, ob sie richtig ist und ich möchte nicht mit einer falschen Grundformel weitermachen. Könntet ihr mir helfen?