Bestimmen Sie die Taylor-Approximation zweiter Ordnung p2 der reellen Funktion g, gegeben durch g(x)=ex-1-x2 +1 im …

Question

Aufgabe:

Bestimmen Sie die Taylor-Approximation zweiter Ordnung p2 der reellen Funktion g, gegeben durch g(x)=e^x-1-x² +1 im Bezugspunkt x ̄ = 1. Bestimmen Sie die Gleichung der Tangente an den Graphen von g ⊆ IR × IR in x ̄ = 1.

Problem/Ansatz:

Wie kann ich das Problem lösen?

Comments

Bitte jemand?

Answer 1

Bestimme z. Bsp. die 1. und 2. Ableitung von \(g\) an der Stelle \(x=1\) und setze in die Formel für das Taylor-Polynom ein.

Die gesuchte Tangente ist dann das Taylor-Polynom 1. Grades.

Comments

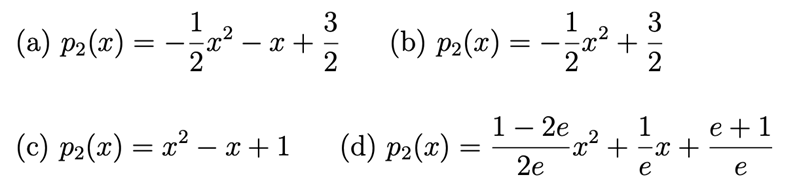
Text erkannt:

(a) \( p_{2}(x)=-\frac{1}{2} x^{2}-x+\frac{3}{2} \)
(b) \( p_{2}(x)=-\frac{1}{2} x^{2}+\frac{3}{2} \)
(c) \( p_{2}(x)=x^{2}-x+1 \)
(d) \( p_{2}(x)=\frac{1-2 e}{2 e} x^{2}+\frac{1}{e} x+\frac{e+1}{e} \)

Als mögliche Lösungen habe ich diese, aber keine davon scheint richtig zu sein? Kannst du mir helfen?

---

Kann ich.
Was hast du denn als 1. und 2. Ableitung von \(g\) heraus?
Das wäre ein erster wichtiger Schritt.

---

Die angegebenen Lösungen entsprechen dem Entwicklungspunkt \(x=0\) und nicht \(x=1\).
Siehe hier.

Damit ist d) richtig.