Hallo zusammen, bei der nachfolgend dargestellten Aufgabe komme ich nicht weiter und ich kann sie nicht bearbeiten. Ich habe am Unterricht teilgenommen und aufgepasst aber komme mit dieser Aufgabe nicht zurecht. Kann mir bitte jemand helfen? Ich brauche im Prinzip nur von einer der vier Aufgaben den Rechenweg. Den Rest kann ich dann übertragen. Die Endlösungen habe ich, die stehen im Buch, aber ohne Rechenweg komme ich nicht weiter.
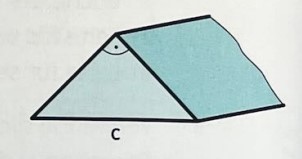
Ein \( 55 \mathrm{~cm} \) langer Dreikant aus Stahl \( \left(\varrho=7800 \mathrm{~kg} / \mathrm{m}^{3}\right) \) hat als Querschnitt ein rechtwinklig-gleichschenkliges Dreieck mit der Hypotenusenlänge c \( (\rightarrow \) Figur). Berechne 1) das Volumen, 2) die Masse!
a) \( \mathrm{c}=15 \mathrm{~mm} \)
b) \( c=1,8 \mathrm{~cm} \)
c) \( c=2,4 \mathrm{~cm} \)
d) \( c=37 \mathrm{~mm} \)
Lösungen:
a) 1) \( V \approx 31 \mathrm{~cm}^{3}(30,9 \ldots) \)
2) \( m \approx 0,24 \mathrm{~kg}(0,241 \ldots) \)
b) 1) \( V \approx 45 \mathrm{~cm}^{3} \underline{(44,55)} \)
2) \( m \approx 0,35 \mathrm{~kg}(0,347 \ldots) \)
c) 1) \( V \approx 79 \mathrm{~cm}^{3}(79,2) \)
2) \( m \approx 0,62 \mathrm{~kg}(0,617 \ldots) \)
d) 1) \( V \approx 188 \mathrm{~cm}^{3}(\underline{188,2 \ldots)} \)
2) \( \mathrm{m} \approx 1,47 \mathrm{~kg}(1,468 \ldots) \)
Lieben Dank im Voraus
Sevi