Zeigen Sie, dass Pr(A ∪B) = Pr(A) + Pr(B) – Pr(A ∩B) gilt.

Question

Aufgabe: Zeigen Sie, dass Pr(A ∪B) = Pr(A) + Pr(B) – Pr(A ∩B) gilt.

Problem/Ansatz:

Ich weiß nicht wie ich da vorgehen soll, bzw. habe ich auch nicht wirklich einen Ansatz. Kann mir da jemand bitte weiterhelfen ?

Comments

https://www.lernhelfer.de/schuelerlexikon/mathematik-abitur/artikel/rechenregeln-fuer-wahrscheinlichkeiten-und-ihre-beweise#

Answer 1

Beweisskizze:

Man zerlegt das Ereignis \(A\cup B\) in unvereinbare Ereignisse \(A\) und \(\overline{A}\cap B\) und führt eine Nulladdition mit dem Ereignis \(A\cap B\) durch. Wegen \((\overline{A}\cap B) \cup (A\cap B)=B\) (diese Ereignisse sind auch unvereinbar) folgt dann die Behauptung.

Benutzt wird hier zweimal \(P(A\cup B)=P(A)+P(B)\) für unvereinbare Ereignisse.

Answer 2

Aloha :)

Willkommen in der Mathelounge... \o/

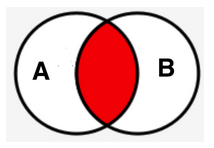
Mit der Wahrscheinlickeit \(P(A)\) liegt das Versuchs-Ergebnis in der Menge \(A\).

Mit der Wahrscheinlickeit \(P(B)\) liegt das Versuchs-Ergebnis in der Menge \(B\).

Gesucht ist die Wahrscheinlichkeit \(P(A\cup B)\), dass das Versuchs-Ergebnis in der Menge \(A\) oder in der Menge \(B\) liegt.

Wenn man \(P(A)\) und \(P(B)\) einfach addiert, werden die möglichen Versuchs-Ergebnisse in der roten Schnittmenge \((A\cap B)\) doppelt gezählt, weil diese Schnittmenge ja in \(A\) und in \(B\) enthalten ist.

Daher ist die Wahrscheinlichkeit \(P(A\cap B)\), dass das Versuchs-Ergebnis in \(A\) und \(B\) zugleich liegt, in der Summe \(P(A)+P(B)\) doppelt enthalten.

Zur Korrektur wird eine der doppelten Wahrscheinlichkeiten \(P(A\cap B)\) wieder subtrahiert:

$$P(A\cup B)=P(A)+P(B)-P(A\cap B)$$