Grad der Funktionen herausfinden?

Question

Hallo,

ist es eigentlich möglich nur anhand einer Grafik (also da ist ein Koordinatensystem und da ist eine Funktion gezeichnet)
Zu erkennen welchen Grad die Funktion hat? z. B. Grad 6 oder 7 

Comments

Es kommt darauf an, was du klar ablesen kannst.

Hast du ein Beispiel parat?

---

\( < \)

Zum Beispiel bei dieser Funktion, kann man den Grad hier herauslesen ohne irgendwelche Rechnungen?

---

Was hast du alles identifiziert?

Wieviel Gleichungen kann man "sicher" aufstellen?

---

Ich hab das nur aus dem Netz die Grafik, wir haben das Thema nur neu angefangen und das Globalverhalten "untersucht"

Dann ist mir einfach so die Frage gekommen, ob man nur anhand der bzw. einer Grafik den Grad der Funktion rauslesen kann.

Answer 1

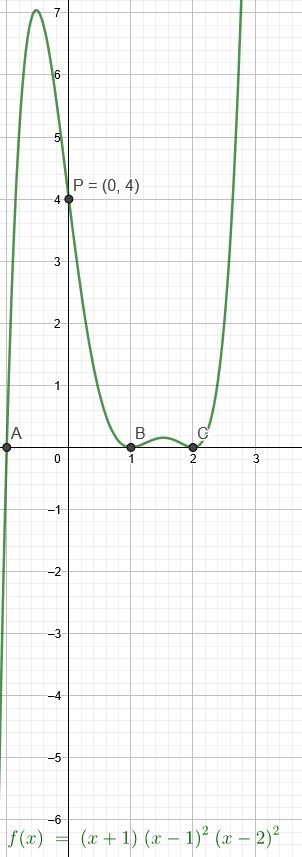
Der Graph auf dem Bild hat bei \(x=-1\) eine einfache Nullstelle, bei  \(x=1\) eine doppelte Nullstelle (Minimum) und bei  \(x=2\) auch eine doppelte Nullstelle Das sind 5 Nullstellen. Wir haben hier eine Funktion 5.Grades

\(f(x)=a(x+1)(x-1)^2(x-2)^2\)

\(P(0|4)\) liegt auf dem Graph von \(f(x)\)

\(f(0)=a(0+1)(0-1)^2(0-2)^2=4a\)

\(4a=4\)

\(a=1\)

\(f(x)=(x+1)(x-1)^2(x-2)^2\)

Wenn du nun ausmultiplizierst, erhältst du \(f(x)=x^\red{5}-5x^4+7x^3+x^2-8x+4\)

\(\red{5} \) ist die höchste Potenz, somit ist der Grad \(\red{5} \)  

Comments

Mindestens Grad 5. Man muss hier einfach etwas vorsichtig sein bzw. sollte das präzise benennen.

---

Der Vergleich mit dem gegebenen Bild zeigt, dass die Lösung richtig ist.

Answer 2

Hallo

da es von -oo zu + unendlich geht, kannst du entscheiden, derGrad ist ungerade, dann zähl die Anzahl der Extrema, dann weisst du wie groß der Grad der Ableitung sicher ist. Damit kann man sagen der Grad ist mindestens... aber er kann auch 2 oder 4 größer sein oder noch mehr.

Gruß lul