Beschränktes Wachstum, explizite Darstellung

Question

Aufgabe:

Ein Bestand B hat den Anfangswert 5000. Es gilt B (n) = B (n - 1) + p (S - B(n -1)), n in Jah-
ren. Geben Sie für B eine explizite Darstellung an und erstellen Sie eine Wertetabelle für n ≤ 10.
a) S = 10000; p = 0,1
b) S = 20000; p = 0,1
c) S = 1000; p = 0,1

Problem/Ansatz:

Kann mir jemand bei der Aufgabe helfen? Ich weiß nicht wo ich anfangen soll.

Comments

wo ich anfangen soll

Finden einer Vermutung für die explizite Darstellung (die dann später durch vst. Ind. bewiesen wird) mittels Einsetzen von B(0) (=Anfangsbestand) in B(1), dann dieses B(1) in B(2), dann dieses B(2) in B(3) ... (Diese sukzessiven Einsetzungen erfolgen mit Termen, nicht mit Zahlenwerten.)
Dabei mag es günstig sein, S-B(n) zu betrachten.

Zur Kontrolle kannst du die so vermutete explizite Formel der gegebenen rekursiven in einer Tabellekalkulation gegenüberstellen (und als Lösung für die gesuchten Werte abschreiben).

Answer 1

z.B. bei a) kann man so vorgehen:

mit S = 10000; p = 0,1 und

Anfangswert 5000 und es gilt B (n) = B (n - 1) + p (S - B(n -1))

      ==> B (n) = B (n - 1) + 0,1 (10000 - B(n -1))

      ==> B (n) = B (n - 1) + 1000 - 0,1 * B(n -1)

                ==> B (n) = 0,9 *B (n - 1) + 1000

==> B(1) =   0,9 * 5000 + 1000

         =  0,9 * 4000 + 0,9 *1000 + 1000

==> B(2) = 0,9 * (  0,9 * 4000 + 0,9 *1000 + 1000 )  + 1000

           = 0,9^2 * 4000 + 0,9^2  *1000 + 0,9*1000  + 1000

           = 0,9^2 * 4000 + 1000 * (  0,9^2  + 0,9^1 + 0,9^0 )

==>  B(3) = 0,9^3 * 4000 + 1000 * ( 0,9^3 + 0,9^2  + 0,9^1 + 0,9^0 )

Jetzt ahnt man schon das Ergebnis

B(n)= 0,9^n * 4000 + 1000 * ( 0,9^n +0,9^(n-1) + ... + 0,9^2  + 0,9^1 + 0,9^0 )

In der Klammer das ist eine geometrische Reihe und da kannst du mit der

Summenformel für die geom. Reihe schreiben

\(  B(n) = 0,9^n \cdot 4000 + 1000 \cdot \frac{0,9^{n+1}-1}{0,9-1}    \)

\(   = 0,9^n \cdot 4000 - 10000 \cdot (0,9^{n+1}-1)   \)

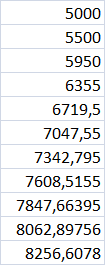
Für die ersten Werte bekomme ich

Text erkannt:

\begin{tabular}{|r}
5000 \\
\hline 5500 \\
\hline 5950 \\
\hline 6355 \\
\hline 6719,5 \\
\hline 7047,55 \\
\hline 7342,795 \\
\hline 7608,5155 \\
\hline 7847,66395 \\
\hline 8062,89756 \\
\hline 8256,6078
\end{tabular}

Comments

Danke! wie kommt man auf 0,9?

    ==> B (n) = B (n - 1) + 0,1 (10000 - B(n -1))

    ==> B (n) = B (n - 1) + 1000 - 0,1 * B(n -1)

              ==> B (n) = 0,9 *B (n - 1) + 1000

---

B (n) = B (n - 1) + 1000 - 0,1 * B(n -1)

= 1000 + B (n - 1)  - 0,1 * B(n -1)

= 1000 + 1 * B (n - 1)  - 0,1 * B(n -1)

= 1000 + (1-0,1) * B (n - 1)  

= 1000 + 0,9 * B (n - 1)