Was ist hier verlangt - Aufgabenstellung?

Question

Untersuchen Sie das Verhalten der Funktionswerte von f für x ⇒±∞

f(x) = 5x - x⁴

Ich verstehe irgendwie nicht was zutun ist, muss ich hier das Globalverhalten angeben?

Answer 1

Der Höchste Exponent von x ist gerade und der Leitkoeffizient ist negativ.

Damit kommt der Graph von links unten und geht nach rechts unten.

Damit kommt der Funktionsgraph aus dem III. Quadranten und verschwindet im IV. Qudranten.

Oder mathematischer

lim (x → -∞) f(x) = -∞
lim (x → ∞) f(x) = -∞

Comments

Könnte man das auch so schreiben weil es ja immer gegen - undelich geht, dann spart man sich ja ein "Schritt "?

\( \lim\limits_{x\to\infty} \)  = ±∞

Unten bei Lim ist auch noch ein ±

---

Hier schreibt man das in der Regel getrennt auf. Ich habe es noch nie gesehen das das zusammengefasst wird zu

lim (x → ±∞) f(x) = -∞

wichtig ist aber das du die Funktion erwähnst, zu der du den Grenzwert angibst. Also hier das f(x)

Answer 2

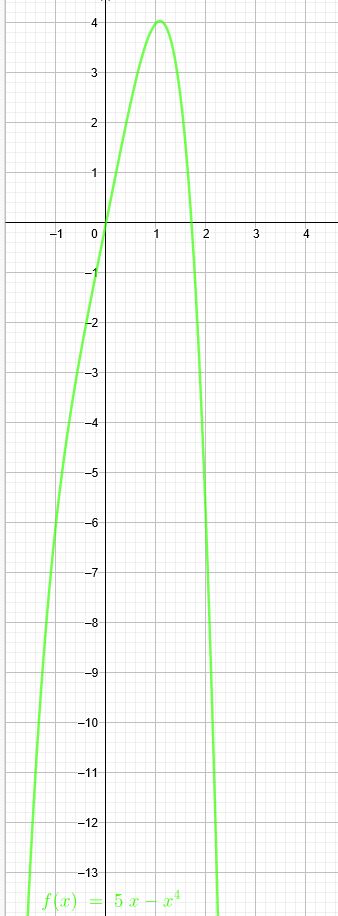
\(f(x) = 5x - x^4\)

Nullstellen:

\( 5x - x^4=0\) → \( x\cdot(5 - x^3)=0\)  → \( x_1=0\) oder   \( x_2=\sqrt[3]{5}≈1,71\)

Extremwert:

\(f'(x) = 5- 4x^3\)   →\( 5- 4x^3=0\)  → \( x=\sqrt[3]{\frac{5}{4}}≈1,08\)    \(f(≈1,08) = 5\cdot 1,08 - 1,08^4≈4,04\)

Die 1.)  Nullstelle ist bei \(x=0\). Die 2.)  Nullstelle ist bei \(x=\sqrt[3]{5}≈1,71\).

Der einzige Extremwert (Maximum) liegt nun eindeutig im 1. Quadrant.

Ich untersuche nun \(f(-10) = 5\cdot(-10) - (-10)^4=-10050\)

Der Punkt ist im 3.Quadranten. →\( \lim\limits_{x\to-\infty} (5x - x^4)=-∞\)

Ich untersuche nun \(f(10) = 5\cdot(10) - (10)^4=-9950\)

Der Punkt ist im 4.Quadranten.→\( \lim\limits_{x\to\infty} (5x - x^4)=-∞\)

Answer 3

muss ich hier das Globalverhalten angeben?

Ja.

Du musst nur -x^4 betrachten, 4x kann man vernachlässigen für x -> +- oo

x^4 ist immer positiv

-> lim f(x) = - oo für x -> +-oo