Griechisches Kreuz zerlegen

Question

Das griechische Kreuz ist aus 5 kongruenten Quadraten zusammengesetzt:

Zerlege es in 4 kongruente Teile, mit denen man ein Quadrat parkettieren kann.

Answer 1

[spoiler]

https://www.spiegel.de/wissenschaft/mensch/raetsel-der-woche-ein-kreuz-muss-dran-glauben-a-1049812.html

[/spoiler]

Comments

Ich würde erst dann im Internet nach Lösungen suchen, wenn ich selbst keine finden kann.

---

Ich kannte die Lösung bereits. Aber vermutlich gilt das nicht für jeden, der hier im Forum liest.

Answer 2

Hallo Roland,

Der Weg ist das Ziel. Es folgt eine Kurzbescheibung des Lösungswegs, den ich genommen habe; denn ich kannte die Lösung vorher noch nicht.

Zunächst hatte ich mir überlegt, wie das finale Quadrat zusammen gesetzt ist, und bin auf zwei Varianten gestoßen

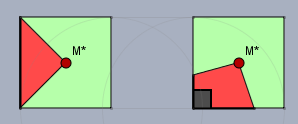
Im ersten Fall (links) deckt eine der vier Teilflächen genau eine Seite ab. Im zweiten Fall enthält eine Teilfläche eine komplette Ecke. Wobei die Seiten der Teilfläche, die den Rand des Quadrates bilden, in Summe eine Länge von \(\sqrt{5}\) haben müssen, wenn die Seitenlänge der 5 Quadrate im Kreuz eine Längeneinheit ist (das muss ich hier jetzt nicht erklären - oder?)

Weiter habe ich angenommen, dass der Mittelpunkt \(M^*\) des Quadrates in jedem Fall Rand- bzw. Eckpunkt der Teilfläche sein muss. Ich ging implizit davon aus, dass im zusammengesetzten Zustand sich die Teilflächen durch Rotationen um je 90° auf einander abbilden lassen. Mit dieser Vorausetzung folgt das sofort.

Die Variante, dass eine Teilfläche eine Seite des Zielquadrats enthält, hatte ich dann irgendwann verworfen.

Bei der zweiten Variante (eine Teilfläche enthält eine Ecke) stellt sich zunächst die Frage: wo sind die Ecken im Kreuz? Mein erster Gedanke sah in etwa so aus:

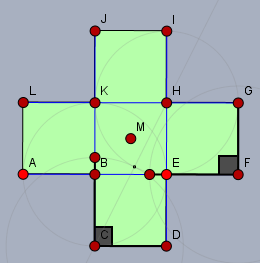
Die Idee ist, dass die Punkte \(C\) und \(F\) in den Ecken des finalen Quadrats landen. Die passenden Seitenstücke habe ich in der Skizze schwarz markiert. Es hat dann eine Weile gedauert, bis ich gesehen habe, dass dies nicht möglich ist. Genau wie beim Quadrat muss man IMHO auch hier davon ausgehen, dass der Mittelpunkt \(M\) Rand- bzw. Eckpunkt jeder der Teilflächen ist. Wenn man nun \(F\) in die Zielposition verschiebt, nimmt man ja den Punkt \(M\), der zwansgläufig auch an dieser Teilfläche hängt, mit. Und die Zielposition von desem Punkt läge dann innerhalb der ersten Teilfläche (\(C\)).

Später fiel mir dann auf, unter der Annahme der Rotationssymmetrie, dass in \(M\) zwangsläufig rechte Winkel auftauchen müssen. Jede der vier Teilflächen hätte in diesem Punkt eine Ecke mit identischem Winkel - also 360°:4 =90°. Diese Überlegung führte dann zu dieser Skizze:

Also nahm ich an, dass \(M\) in den Ecken des finalen Quadrats landet. Und - um es einfach zu machen - nahm ich auch an, dass die nötigen Schnitte (die roten Geraden) bis zu den Rändern des Kreuzes gerade sind. Mussten sie ja sein, weil diese Geraden sind später die Seiten des finalen Quadrats.

Der Schnitt geht dann vom Punkt \(X\) über \(M\) bis \(Y\). Die Länge des Zuges von \(X\) über \(M\) bis \(S\) ist \(\sqrt{5}\). Folglich muss man \(X\) so verschieben, dass \(S\) und \(Y\) zusammen fallen - bzw. die rote Teilstrecke \(SY\) verschwindet.

Und dies ist genau dann der Fall, wenn \(X\) in der Mitte von \(EF\) liegt. Dann fiel mir auch auf, dass die Strecke \(|YC|\) und \(|EX|\) gleich lang sein müssen, damit die Teilflächen später auch ohne Lücke zusammen passen. Und da \(|BY|=|EX|\) ist, müssen \(X\) und \(Y\) in den Mitten von \(BF\) und \(BC\) liegen.

Damit hatte ich eine Lösung gefunden! Man muss zwar jetzt noch ein wenig überprüfen, aber das ist Kleinkram, die Erklärung lasse ich hier weg. Und so sieht's aus:

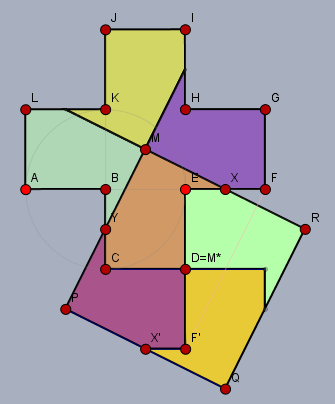
Später sind mir dann noch 'ne Menge anderer Gesetzmäßigkeiten ein- und aufgefallen. Aber das überlasse ich dem werten Leser.

Wirklich eine schöne Aufgabe, die wieder mal zeigt: man lernt Mathematik nicht durch zusehen, man muss es selber machen. Sie ist mehr ein Tun als eine Lehre.

Gruß Werner