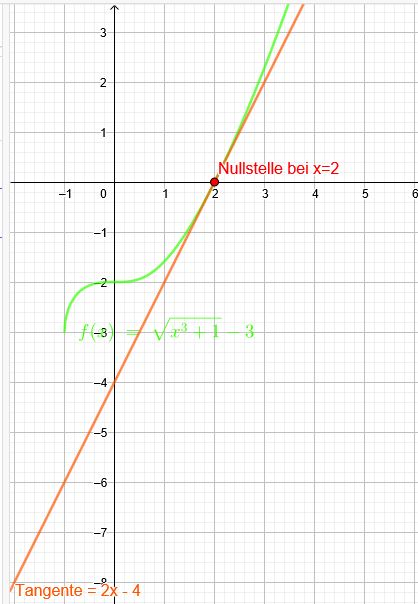
Gegeben ist die Funktion \( \mathrm{f}(\mathrm{x})=\sqrt{\mathrm{x}^{3}+1}-3 \).
\(a_1\) Definitionsmenge:
\( {x}^{3}+1≥0 \)
\(a_2\) die Nullstelle von \( f \) :
\(\sqrt{\mathrm{x}^{3}+1}-3=0 \)
\(\sqrt{\mathrm{x}^{3}+1}=3 |^{2} \)
\(x^3+1=9 \)
\(x^3=8 |\sqrt[3]{~~} \)
\(x=2 \) Die anderen beiden Lösungen liegen nicht in ℝ
b)
Bilden Sie die Ableitung f , mithilfe der allgemeinen Kettenregel
\(f(x)=\sqrt{x^3+1} -3\)
\(f'(x)=\frac{3x^2}{2 \cdot \sqrt{x^3+1} } =\frac{1,5x^2}{ \sqrt{x^3+1} } \)
c)
Bestimmen Sie die Gleichung der Nullstellentangente von \( \mathrm{f} \).
\(f'(2)=\frac{1,5\cdot 2^2}{ \sqrt{2^3+1} }= 2\)
\( \frac{y-0}{x-2}=2 \)
\( y=2x-4 \)