Man sollte die Brüche soweit wie möglich kürzen. Dies macht man am besten, in dem man den Bruchstrich durchzieht (dort wo es mal ist) und das Multiplikationszeichen über und unter den strich an der gleichen stelle schreibst:
$$ \begin{array} { l } { \frac { 4 x y } { 6 a ^ { 2 } b ^ { 2 } } \times \frac { 7 a b } { x ^ { 3 } y ^ { 4 } } + \frac { 9 a ^ { 4 } b } { 12 x ^ { 2 } y ^ { 6 } } \times \frac { 11 y ^ { 6 } } { 12 a ^ { 5 } b ^ { 6 } } = } \\ { \frac { 4 x y \times 7 a b } { 6 a ^ { 2 } b ^ { 2 } \times x ^ { 3 } y ^ { 4 } } + \frac { 9 a ^ { 4 } b \times 11 y ^ { 6 } } { 12 x ^ { 2 } y ^ { 6 } \times 12 a ^ { 5 } b ^ { 6 } } = } \end{array} $$
Nun kann man wie gewohnt kürzen und die mals weglassen (da man sowieso mal rechnet...):
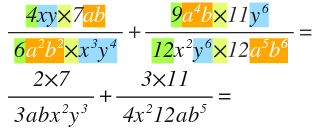
Dies kann man noch weiter ausrechnen und man muss nun so erweitern, dass der Nenner gleich wird. Zum Schluss kürzt man, indem man ausklammert:
$$ \begin{array} { l } { \frac { 14 } { 3 a b x ^ { 2 } y ^ { 3 } } + \frac { 33 } { 48 a b ^ { 5 } x ^ { 2 } } = } \\ { \frac { 14 \times 48 a b ^ { 5 } x ^ { 2 } + 3 a b x ^ { 2 } y ^ { 3 } \times 11 } { 3 a b x ^ { 2 } y ^ { 3 } \times 48 a b ^ { 5 } x ^ { 2 } } = } \end{array} \\ \begin{array} { l } { \frac { 168 a b ^ { 5 } x ^ { 2 } + 33 a b x ^ { 2 } y ^ { 3 } } { 36 a b x ^ { 2 } y ^ { 3 } \times 48 a b ^ { 5 } x ^ { 2 } } = } \\ { \frac { 24 a b x ^ { 2 } \times \left( 7 b ^ { 4 } + 2 y ^ { 3 } \right) } { 144 a ^ { 2 } b ^ { 6 } x ^ { 4 } y ^ { 3 } } = } \end{array} \\ \frac { 7 b ^ { 4 } + 2 y ^ { 3 } } { 6 a b ^ { 6 } x ^ { 2 } y ^ { 3 } } $$
Dies ist schon die Lösung.