´Hallo, ich habe ziemliche Probleme den Flächenschwerpunkt zu bestimmen bzw allgemein mit der Formel. Leider haben wird dazu nichts in der Vorlesung gemacht.
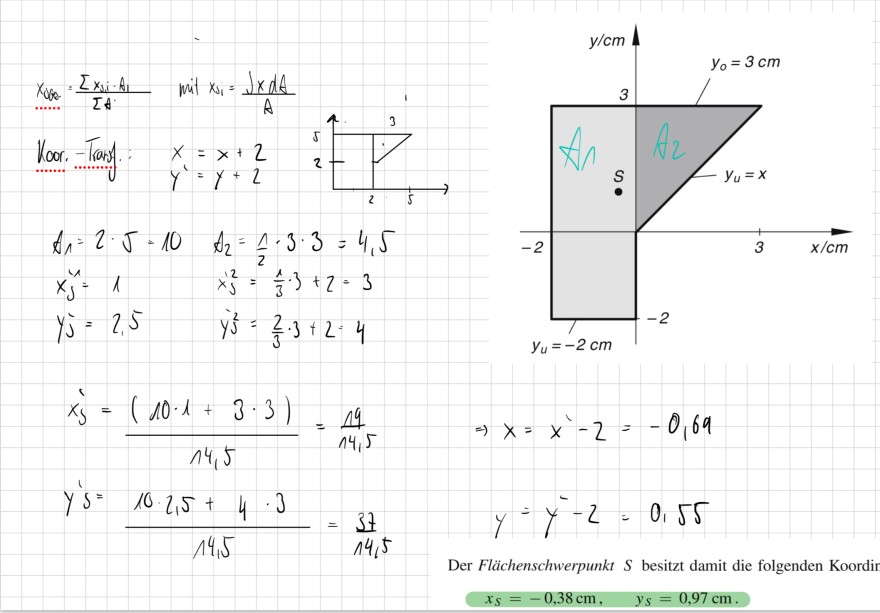
Also ich würde gern den SP dieser Teilflächen (siehe Bild) bestimmen. Mein Ansatz ist dem Bild zu entnehmen. Meine Lösung ist falsch. In der Lösung wurde auch mit der in Rot markierten Formel gerechnet. Wieso? Was habe ich falsch gemacht? Wann verwende ich welche Formel?
Aufgabenstellung & mein Ansatz:
Formel-Musterlösung:

Text erkannt:
Schwerpunkt einer homogenen ebenen Fläche zwischen zwei Kurven (Bild V-82)
Die Koordinaten \( x_{S} \) und \( y_{S} \) des Schwerpunktes einer homogenen ebenen Fläche, die von den Kurven \( y_{o}=f_{o}(x) \) und \( y_{u}=f_{u}(x) \) und den beiden Parallelen \( x=a \) und \( x=b \) berandet wird, lassen sich wie folgt berechnen:
\( \begin{array}{l} x_{S}=\frac{1}{A} \cdot \int \limits_{a}^{b} x\left(y_{o}-y_{u}\right) d x=\frac{1}{A} \cdot \int \limits_{a}^{b} x\left[f_{o}(x)-f_{u}(x)\right] d x \\ y_{S}=\frac{1}{2 A} \cdot \int \limits_{a}^{b}\left(y_{o}^{2}-y_{u}^{2}\right) d x=\frac{1}{2 A} \cdot \int \limits_{a}^{b}\left[\left(f_{o}(x)\right)^{2}-\left(f_{u}(x)\right)^{2}\right] d x \end{array} \)
A: Flächeninhalt, berechnet nach der Integralformel (V-122)
Voraussetzung: \( f_{o}(x) \geq f_{u}(x) \) im Intervall \( a \leq x \leq b \)