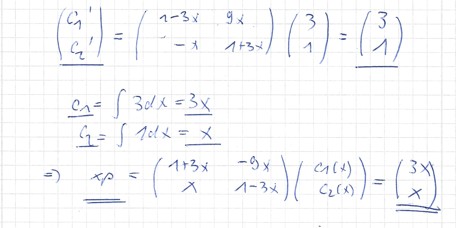partikuläre Lösung DGL-System

Question

Aufgabe:

Ich habe eine Matrix $$ Y(x)=\begin{pmatrix} 1+3x & -9x \\ x & 1-3x \end{pmatrix} $$gegeben. Diese ist Fundamentalsystem von y'=Ay mit $$ A=\begin{pmatrix} 3 & -9 \\ 1 & -3 \end{pmatrix} $$. Ich soll eine partikuläre Lösung $$ y_{p} $$ des DGL-Systems y'(x)=Ay(x)+b(x) für $$ b(x)=\begin{pmatrix} 3\\1 \end{pmatrix} $$bestimmen.

Problem/Ansatz:

Ich weiß das Y(0)=E ist und damit gilt $$ Y(x)=e^{x \cdot A }$$. Dann kann ich die Variation-der-Konstanten-Formel anwenden. Da ist ja der Ansatz: $$ y_{p}(x)=\int \limits_{}^{x}e^{(x-z) \cdot A}*b(z)dz $$. Jetzt weiß ich aber nicht wie ich damit weiterrechnen soll. Kann mir da jemand helfen?

Comments

Ist Dir klar, dass

Exp((x-z)A)=Y(x)[Y(z)]^(-1)

Ist? Damit kannst Du den Integranden berechnen und dann integrieren. Ich würde den Faktor Y(x) vor das Integral ziehen.

---

und was nehme ich als Y(z)?

---

Du hast doch selbst Y angegeben?!

---

$$\begin{pmatrix} 1+3*x & -9x \\ x & 1-3x \end{pmatrix} \int \limits_{0}^{x}\begin{pmatrix} 1+3z & -9z \\ z & 1-3z \end{pmatrix}^{-1}*\begin{pmatrix} 3\\1 \end{pmatrix}$$ dz =

$$\begin{pmatrix} 1+3*x & -9x \\ x & 1-3x \end{pmatrix} \int \limits_{0}^{x}\begin{pmatrix} 1-3z & 9z \\ -z & 3z+1 \end{pmatrix}*\begin{pmatrix} 3\\1 \end{pmatrix}$$ dz =

$$\begin{pmatrix} 1+3x & -9x \\ x & 1-3x \end{pmatrix}\int \limits_{0}^{x}\begin{pmatrix} 3\\1 \end{pmatrix}$$ dz =

$$\begin{pmatrix} 1+3x & -9x \\ x & 1-3x \end{pmatrix}*\begin{pmatrix} 3x\\x \end{pmatrix}$$ =

$$\begin{pmatrix} 3x\\x \end{pmatrix}$$

Habe ich das dann so richtig gerechnet?

---

Mach doch einfach die Probe.

Answer 1

Hallo,

deine partikuläre Lösung ist richtig.

Wolfram alpha bestätigt das.

https://www.wolframalpha.com/

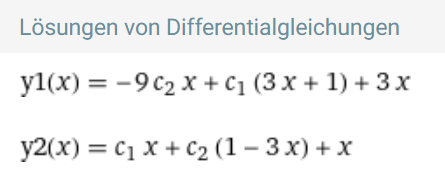
ich habe auch via Variation der Konstanten gerechnet , der Weg ist etwas anders:

Prinzipiell mußt Du das natürlich so rechnen, wie Ihr das hattet.

(habe kein Fehler gefunden)

Ich habe aber in der Aufgabe nicht speziell gelesen, welcher Weg genau vorgeschrieben wurde.

Comments

Warum schreibst Du die Lösung des FS noch einmal ab?

---

Wie Du siehst , habe ich einen anderen Weg ohne diese Formel genommen.

Abschreiben ist das ja wohl nicht. Außerdem bin ich Dir keine Rechenschaft schuldig , was ich mache.  Das Forum gehört Dir nicht allein. Hier kann jeder antworten

---

Hier kann jeder antworten und jeder kann nach dem Sinn einer Antwort fragen.