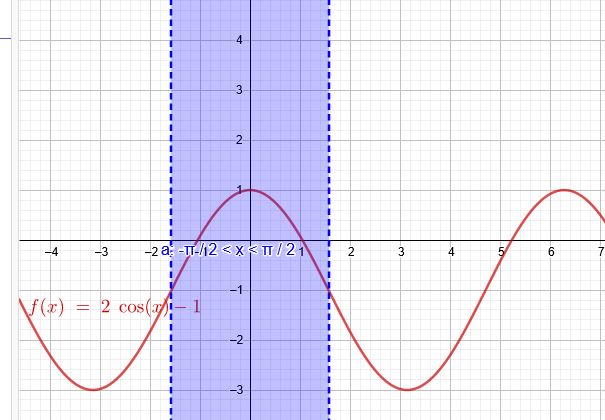
Bestimme die Extrem- und Wendepunkte der Funktion \(f(x) = 2cos x - 1\), \(- \frac{π}{2}<x<\frac{π}{2}\)
Extrempunkte: → \(f'(x) =0) \)
\(f'(x) =- 2sin (x) \)
\(- 2sin (x)=0 \)
\(sin (x)=0 \)
\(x=0 \) \(f(0) = 2cos (0) - 1=1\) wobei \(cos (0)=1 \) \(2cos (0)=2\) ist
Art des Extremwertes:
\(f''(x) =- 2cos(x)\)
\(f''(0) =- 2cos(0)=-2<0\) →Maximum
Wendepunkte: → \(f''(x) =0) \)
\(f''(x) =- 2cos(x)\)
\(- 2cos(x)=0\)
\(cos(x)=0\)
\(x_1=- \frac{π}{2}\) \(f(- \frac{π}{2}) = 2cos (- \frac{π}{2}) - 1=-1\) wobei \(cos (- \frac{π}{2}=0\) ist.
\(x_2= \frac{π}{2}\) \(f(\frac{π}{2}) = 2cos ( \frac{π}{2}) - 1\) wobei \(cos ( \frac{π}{2}=0\) ist.
Wäre dann im Definitionsbereich, wenn \(- \frac{π}{2}≤x≤\frac{π}{2}\) gelten würde.