Grafisches Ableiten - Frage dazu

Question

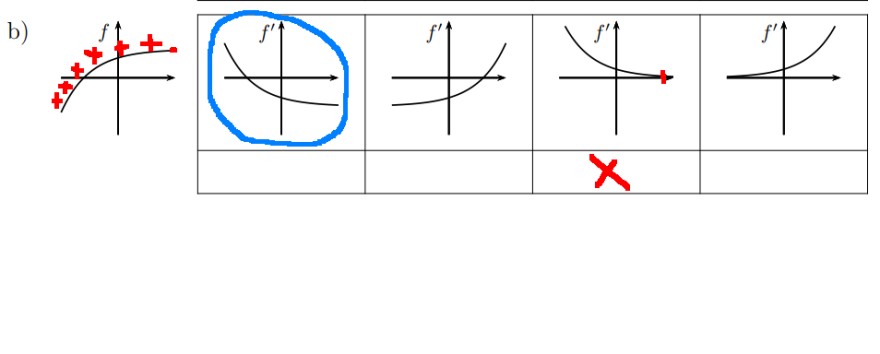
Ich soll zu der gegebenen Zeichnung f(x) grafisch f'(x) bilden.

Habe ich das so richtig gemacht: am Ende des Graphen von f(x) verläuft die Steigung gegen 0, daher habe ich bei f'(x) an dieser Stelle, aber auf der x-Achse (also gleicher y-Wert) eine Markierung gesetzt. Danach habe die Stellen bis zum Ende des Graphen von f(x) betrachtet und sehe, dass permanent eine Steigung vorliegt (daher auch die ganzen roten Plusse).

Also weiß ich, dass wir von oben (also im pos. Bereich) kommen und bis zur gesetzten Stelle bei f'(x) laufen.

So, sollte das obige richtig sein, hier die eigentliche Frage: Wie müsste f(x) aussehen, wenn ich das blau umrundende Bild auswählen würde bzw. was der Unterschied bei f(x) wäre, wenn das blau umrundete Bild die tatsächliche Ableitung wäre.

Answer 1

Die passende Funktion \(f\) zu der von dir markierten Ableitung muss an der Nullstelle der Ableitung einen Hochpunkt haben (VZW von + nach -). Das könnte zum Beispiel sowas in der Art sein wie \(f(x)=-\frac{1}{2}\mathrm{e}^{-\frac{1}{2}x}-x\).

Comments

~plot~ 2^(-0.5x)-3;-2/ln(2)*2^(-0.5x)-3x+2/ln(2) ~plot~

---

Aber meine Überlegungen sind soweit richtig, ja?
Also wie ich auf die richtige Lösung gekommen bin.

---

Ja.

Da f(x) streng monoton steigend ist darf f'(x) nur positive Funktionswerte haben. Damit kann man also die beiden ersten Graphen schon ausschließen.

Da die Steigung von f(x) nach rechts hin immer flacher wird, müssen die Funktionswerte abnehmen. Das spricht dann für den dritten Graphen.

Answer 2

Hallo

Du sollst nicht graphisch ableiten, sonder aus den 4 gegebenen f' Abbildungen eine passende zu dem gegebenen f aussuchen,  mit der rot angekreuzten hast du das richtig gemacht,

zur blauen f' : zuerst steigt die Funktion hat dann ein Maximum, wo f'=0 und fällt dann  immer stärker.

Gruß lul