Aufgabe:

Text erkannt:
Bel einer Wahl, bel der 7 Sitze zu vertellen sind, ergaben sich folgende Stimmvertellungen:
Partei A: 3000 Stimmen, Partei B: 4000 Stimmen, Partei C: 6000 Stimmen.
1. Wir betrachten das d'Hondt-Verfahren.
(a) Bestimmen Sie die Anzahl der Sitze, die jede Partei bekommt, wenn die Sitze nach dem d'HondtVerfahren verteilt werden. Benutzen Sie dafür das Höchstzahlverfahren.
(b) Bestimmen Sie die für diese Sitzverteilung möglichen Divisoren.
(c) Benutzen Sie nun einen dieser Divisoren um mit der Divisormethode erneut die Sitzverteilung zu bestimmen.
(d) Bestimmen Sie den Sitzexzess jeder Partei.
Problem/Ansatz:
Kann mir jemand verraten, ob ich die Aufgabe bisher korrekt bearbeitet habe und wie ich den Sitzexzess bei d.) ausrechne?

Text erkannt:
Aufgabe 1
Bei einer Wahl, bei der 7 Sitze zu verteilen sind, ergaben sich folgenden Stimmverteilung
Partei A: 3000 Stimmen
Partei B: 4000 Stimmen
Partei C: 6000 Stimmen
1.) Wir betrachten das d'Hondt - Verfahren
a) Bestimmen Sie die Anzahl der Sitze, die jede Partei bekommt, wenn die Sitze nach dem d'Hondt Verfahren verteilt werden. Benutzen Sie dafür das Höchstzahlverfahren.
Text erkannt:
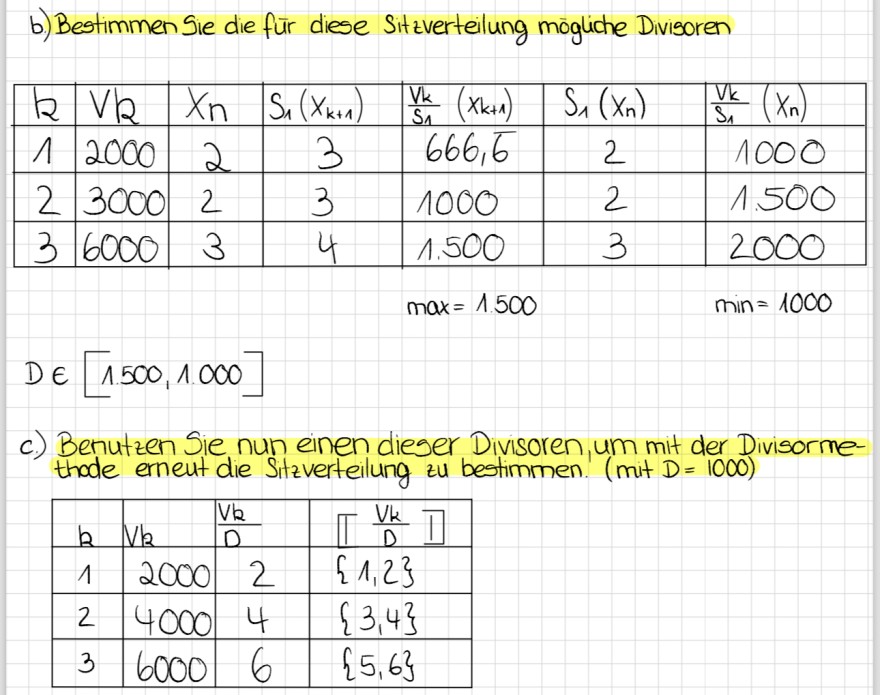
b) Bestimmen Sie die für diese Sitzverteilung mögliche Divisoren
\begin{tabular}{|c|c|c|c|c|c|c|}
\hline\( k \) & \( V k \) & \( X_{n} \) & \( S_{1}\left(X_{k+1}\right) \) & \( \frac{V_{k}}{s_{1}}\left(x_{k+1}\right) \) & \( S_{1}\left(X_{n}\right) \) & \( \frac{V_{k}}{s_{1}}\left(X_{n}\right) \) \\
\hline 1 & 2000 & 2 & 3 & \( 666, \overline{6} \) & 2 & 1000 \\
\hline 2 & 3000 & 2 & 3 & 1000 & 2 & 1.500 \\
\hline 3 & 6000 & 3 & 4 & 1.500 & 3 & 2000 \\
\hline
\end{tabular}
\( \max =1.500 \)
\( \min =1000 \)
\( D \in[1.500,1.000] \)
c.) Benutzen Sie nun einen dieser Divisoren, um mit der Divisormethode erneut die Sitzverteilung zu bestimmen. (mit \( D=1000 \) )
\begin{tabular}{|c|c|c|c|}
\hline\( k \) & \( V_{k} \) & \( \frac{V_{k}}{D} \) & \( \llbracket \frac{V_{k}}{D} \rrbracket \) \\
\hline 1 & 2000 & 2 & \( \{1,2\} \) \\
\hline 2 & 4000 & 4 & \( \{3,4\} \) \\
\hline 3 & 6000 & 6 & \( \{5,6\} \) \\
\hline
\end{tabular}