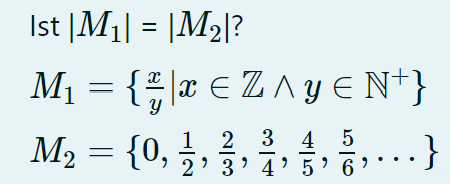
Text erkannt:
\( \begin{array}{l}\text { Ist }\left|M_{1}\right|=\left|M_{2}\right| ? \\ M_{1}=\left\{\left.\frac{x}{y} \right\rvert\, x \in \mathbb{Z} \wedge y \in \mathbb{N}^{+}\right\} \\ M_{2}=\left\{0, \frac{1}{2}, \frac{2}{3}, \frac{3}{4}, \frac{4}{5}, \frac{5}{6}, \ldots\right\}\end{array} \)
Hallo Leute,
Habe diese Aufgabe und würde aus meinem Gefühl sagen das M1 nicht gleich M2 ist.
Aber die Musterlösung sagt anderes :I
Nun verstehe ich aber nicht wie die Kardinalität gleich sein soll wen x bei M1 Element von Z ist.
Dadurch werden doch Negative Brüche mit eingeschlossen oder nicht und somit müsste M1 > M2 sein ?