Question

Muss man bei solchen Aufgaben zuerst skalieren und dann verschieben oder zuerst verschieben und dann skalieren? Weil, wenn ich zuerst skaliere und dann verschiebe, komme ich nicht ganz auf die Lösung (für den unwahrscheinlichen Fall kann auch die Lösung falsch sein, allerdings bezweifle ich das).

Geht hier um die letzten Graphen d) bzw. "f)" wie es in der Lösung aufm Bild steht.

Answer 1

Man sucht das \(x\) und schaut schrittweise, was mit dem gemacht werden muss um zum Gesamtausdruck zu kommen. Dann wird auch der Unterschied zwischen \(2x+5\) und \(2(x+5)\) klar betr. Reihenfolge der Operationen.

Comments

Ja, du nennst das Problem beim Wort: "und schaut schrittweise".

Ich weiß ja eben nicht, welche Schritte ich in welcher Reihenfolge zu befolgen habe...

---

Welche Schritte, in welcher Reihenfolge, musst Du denn mit \(x\) ausführen, um

a) auf \(2x+5\) zu kommen

b) auf \(2(x+5)\) zu kommen?

---

a) Den Graphen um 2 Einheiten in y-Richtung strecken und dann um 5 Einheiten nach links verschieben.

b) Den Graphen um 5 Einheiten nach links verschieben und dann um 2 Einheiten in y-Richtung strecken.

So korrekt?

---

Von der Idee her: ja. Aber von Graphen war noch nicht die Rede - ist doch noch kein \(f\) drin, nur von Zahlen. Daher geht es in dieser Vorübung auch nicht um x- oder y-Richtung und links/rechts-Verschiebung.

---

Ok, ich verstehe das so, dass du darauf hinaus möchtest, dass ich zunächst die Klammer "berechnen" soll. a) wäre 2x + 5 und b) 2x + 10

So habe ich es auch versucht, in der obigen Aufgabe zu machen: Ich habe zunächst 1/2x betrachtet (also entspr. skaliert) und dann entspr. verschoben. Allerdings muss man zuerst verschieben und dann skalieren (wenn ich mir die Lösung mal so anschaue). Ich kann mir halt leider nicht erklären, wieso das so ist...

---

Es gibt immer mehrere Möglichkeiten, das siehst Du auch am Beispiel:

2x+5: mal 2, plus 5

2(x+5): plus 5, mal 2, aber auch: mal 2, plus 10.

Im Beispiel d)/f): die Veränderungen spielen sich nur auf der x-Achse ab (da sie im Argument von \(f\) stehen).

\(f(\frac12x+2)\):

Faktor 1/2: Streckung in x-Richtung (Dehnung). Danach +2: Verschiebung in x-Richtung um 2 nach links.

---

Faktor 1/2: Streckung in x-Richtung (Dehnung). Danach +2: Verschiebung in x-Richtung um 2 nach links.

Genau so habe ich das ja auch gemacht!

Ich habe zuerst die x-Werte mit *2 multipliziert, um in x-Richtung dehnen zu können und danach habe ich um 2 Einheiten nach links verschoben

Dann sieht es auch bei mir so aus:

---

Du hast recht, das geht so nicht und ich hab das nun nochmal gründlich durchgedacht (danke für die Anregung).

Wenn man \(\frac12x+2=\frac12(x+4)\) bedenkt und dementsprechend vorgeht (um 4 nach links verschieben, danach mit 2 dehnen), kommt man auf das richtige Ergebnis.

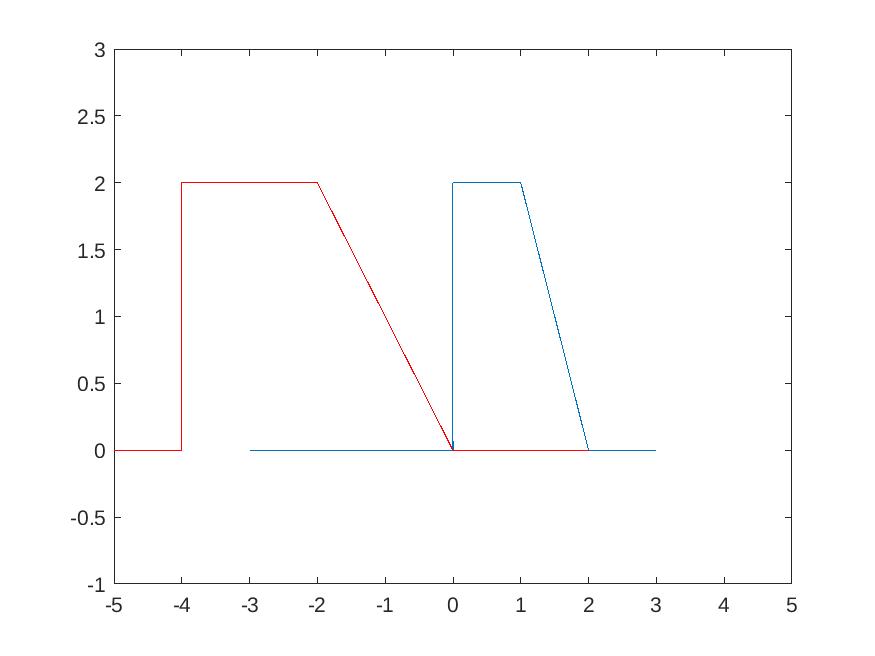
rot ist das Ergebnis, blau die Ausgangsfunktion.

Schauen wir uns das andere (erst dehnen, dann verschieben) mal schrittweise an:

Erster Schritt - dehnen: \(h(x)=f(\frac12x)\): Ergebnis wie erwartet.

Wenn wir nun aber \(h\) um 2 nach links schieben (um mutmaßlich \(f(\frac12x+2)\) zu erhalten), erhalten wir \(h(x+2)=f(\frac12(x+2))=f(\frac12x+1)\). Das wollten wir aber nicht!

Um unser Ziel zu erreichen, müssen wir \(h\) um 4 nach links schieben:

\(h(x+4)=f(\frac12(x+4)) =f(\frac12x+2)\).

Der Dehnungsfaktor muss also bei der Verschiebung berücksichtigt werden.

---

Ok, sehr schön erklärt, vielen Dank!

Bei solchen Aufgaben werde ich von nun die Funktion vereinfachen

---

Wobei, jetzt nach dem Probieren geht das glaube ich doch nicht: wenn ich zuerst um 4 Einheiten nach links verschiebe und dann um 2 Strecke, komme ich so nicht auf das Ergebnis

---

Gut, dass Du das alles überprüfst. Du hast wieder recht. Schrittweise:

Man muss erst um 2 verschieben: \(h(x)=f(x+2)\), dann um 2 dehnen: \(h(\frac12x)=f(\frac12x+2)\). Das nachträgliche Dehnen bewirkt, dass die Kante links von \(-2\) (wo sie nach der Verschiebung nach links um \(2\) steht) auf \(-4\) gedehnt wird.

Und nun ist es so, dass es wirklich verwirrend aussieht. Denn obwohl \(x\) erst mit \(\frac12\) multipliziert wird und dann erst \(2\) addiert, muss man zuerst um \(2\) verschieben und dann dehnen.

Leider hab ich wohl oben auch gut zur Verwirrung beigetragen. Bitte um Entschuldigung.

Das Bild oben sollte aber stimmen. Die falschen Erklärungen oben kann ich nicht mehr korrigieren.

Die beiden schrittweisen Erklärungen mit der Zwischenfunktion \(h\) sollten stimmen.

---

Ok, danke für den Nachtrag.

Aber dann kommen wir ja zur Eingangsfrage zurück: Wieso wird zuerst gedehnt und dann erst verschoben?

Klar, den Grund hast du schon oben indirekt genannt:

Das nachträgliche Dehnen bewirkt, dass die Kante links von −2 (wo sie nach der Verschiebung nach links um 2 steht) auf −4 gedehnt wird.

Aber ich kann ja in der Prüfung schlecht die Lösung sehen oder falsche Dehnungen nachträglich (aufgr. der Zeit) korrigieren.

Kann ich es mir denn i.A. so merken, dass immer zuerst gedehnt und dann erst verschoben wird?

---

Kann ich es mir denn i.A. so merken, dass immer zuerst gedehnt und dann erst verschoben wird?

Nicht ganz. Bei der x-Richtung ist es anders als bei der y-Richtung.

Ich wollte noch eine kurze prägnante Zusammenfassung schreiben, aber oswalds Antwort unten macht das schon, daher hab ich das nicht mehr gemacht. Und er hat das auch so gemacht, dass man (ich) es kaum besser machen kann.

Insb. siehst Du da: in x-Richtung erst verschieben, dann strecken. In y-Richtung genau andersrum.

Die Erklärung, warum es so ist, findest Du oben in unserem Dialog.

Answer 2

Der Graph von

        \(g(x) = a\cdot f(\frac{1}{b}\cdot x-d)+e\)

entsteht aus dem Graphen von \(f\) indem dieser

1. horizontal um \(d\) verschoben wird,
2. horizontal mit dem Faktor \(b\) gestreckt wird,
3. vertikal mit dem Faktor \(a\) gestreckt wird,
4. vertikal um \(e\) verschoben wird,
   

und zwar in dieser Reihenfolge.

Dabei gilt

• \(d>0,e>0\): Der Graph wird in die positive Richtung verschoben, ansonsten in die negative Richtung
  
• \(|a|>1,|b|>1\): Der Graph wird auseinandergezogen, ansonsten wird er zusammengedrückt.
• \(a<0,b<0\): Der Graph wird an der Achse gespiegelt.

Für f) heißt das, dass \(f\) zuerst um 2 nach links verschoben und dann mit dem Faktor 2 gestreckt wird.