Vollständige Induktion mit korrekter Notation

Question

Aufgabe:

Beweisen durch vollständige Induktion: (s. Foto)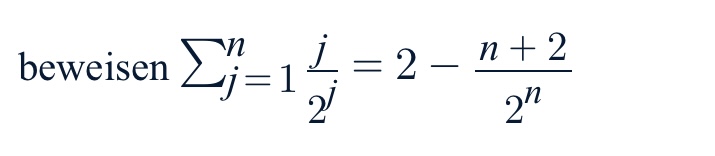

Den Induktionsanfang habe ich hinbekommen. Beide Seiten für n=1 ergeben 1/2

Voraussetzung ist doch eigentlich genau das was auch angegeben ist oder irre ich mich da.

Und Behauptung doch folgendes: n/2^n + (n+1)/2^(n+1) = 2-((n+1+2)/(2^(n+1)))

Mir geht es vor allem um die korrekte Mathematische Notation der Aufgabe mit Induktions-Behauptung und dem eigentlichen Beweis.

Vielen Dank schonmal ;)

Comments

Die Formel ist (in der gelieferten Foto) graphisch ausgesprochen schlecht und damit unverständlich dargestellt.

Answer 1

Hallo

die Ind Vors ist doch 2-(n+1)/2^n dazu wird beim Beweis (n+1)/2ⁿ⁺¹ addiert was rauskommen soll hast du wieder richtig.

Gruß lul

Answer 2

Voraussetzung ist doch eigentlich genau das was auch angegeben ist ...

Nein.

Angegeben ist:

        Für jedes \(n\in \mathbb{N}\) gilt \(\sum\limits_{j=1}^n \frac{j}{2^j}=2-\frac{n+2}{2^n}\).

Induktionsvoraussetzung ist:

        Sei \(n\in \mathbb{N}\), so dass \(\sum\limits_{j=1}^n \frac{j}{2^j}=2-\frac{n+2}{2^n}\) gilt.

Dass ein solches \(n\) existiert, wurde am Induktionsanfang gezeigt.