Hallo,
da habe ich etwas anderes:
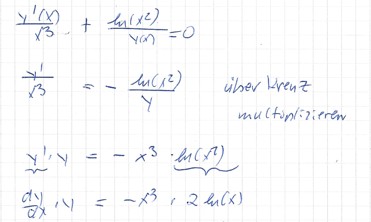
y dy = -\( x^{3} \) *2 ln(x) dx
Das rechte Integral wird via partieller Integration gelöst.
\( \frac{y^{2}}{2}=-\frac{x^{4}(4 \ln (x)-1)}{8}+c \)
nach y umgestellt:
\( y_{1 / 2}= \pm \frac{1}{2} \sqrt{x^{4}-4 x^{4} \ln (x)+8 c} \)
Aufgrund der Anfangsbedingung entfällt die negative Lösung.
Die Anfangsbedingung in die Lösung eingesetzt , ergibt C=0
->Endergebnis:
\( y=\frac{1}{2} \sqrt{x^{4}(1-4 \ln (x))} \)