Aufgabe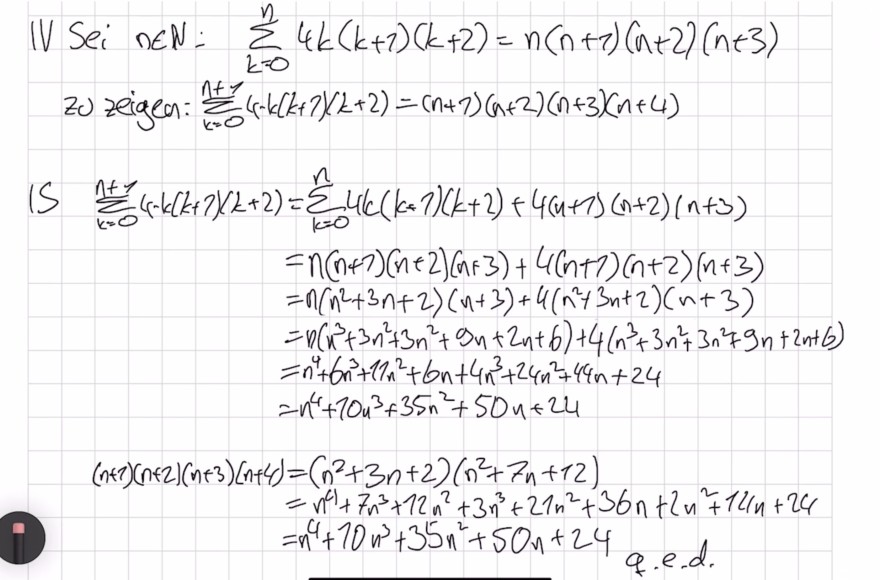
Text erkannt:
IV Sei \( n \in N: \sum \limits_{k=0}^{n} 4 k(k+7)(k+2)=n(n+1)(n+2)(n+3) \)
zo zeigen: \( \sum \limits_{k=0}^{n+1}(r-k(k+7)(k+2)=(n+7)(n+2)(n+3)(n+4) \)
is
\( \begin{aligned} \sum \limits_{k=0}^{n+1}(4-k(k+7)(k+2) & =\sum \limits_{k=0}^{n} 4(k(k+1)(k+2)+4(n+1)(n+2)(n+3) \\ & =n(n+7)(n+2)(n+3)+4(n+7)(n+2)(n+3) \\ & =n\left(n^{2}+3 n+2\right)(n+3)+4\left(n^{2}+3 n+2\right)(n+3) \\ & =n\left(n^{3}+3 n^{2}+3 n^{2}+9 n+2 n+6\right)+4\left(n^{3}+3 n^{2}+3 n^{2}+9 n+2 n+6\right) \\ & =n^{4}+6 n^{3}+1 n^{2}+6 n+4 n^{3}+24 n^{2}+44 n+24 \\ & =n^{4}+10 n^{3}+35 n^{2}+50 n+24 \\ (n+1)(n+2)(n+3)(n+4) & =\left(n^{2}+3 n+2\right)\left(n^{2}+7 n+12\right) \\ & =n^{4}+7 n^{3}+12 n^{2}+3 n^{3}+21 n^{2}+36 n+2 n^{2}+14 n+24 \\ & =n^{4}+10 n^{3}+35 n^{2}+50 n+24 \text { q.e.d. } \end{aligned} \)
Problem/Ansatz
Was wäre hier ein eleganterer Weg, um die Gleichheit zu zeigen?