Aloha :)
Wenn du eine Funktion \(f(x)\) im Intervall \(x\in[a;b]\) um die x-Achse rotierst, entsteht an jeder Stelle \(x\) ein Kreis, dessen Mittelpunkt auf der x-Achse liegt. Der Radius dieses Kreises ist gleich dem Funktionswert, also \(r=f(x)\). Dann ist die Fläche dieses Kreises \(\pi\,r^2=\pi\,f^2(x)\). Das Volumen des entstehenden Rotationskörpers erhältst du, indem du die Fläche aller dieser Kreise entlang der x-Achse summierst:$$V=\int\limits_{x=a}^b\pi\,f^2(x)\,dx$$
zu a) Zylinder
Rotiere die konstante Funktion \(f(x)=r=\text{const}\) im Intervall \(x\in[0;h]\) um die x-Achse:$$V=\int\limits_{x=0}^h\pi\,r^2\,dx=\pi\,r^2\int\limits_{x=0}^hdx=\pi\,r^2\left[x\right]_{x=0}^h=\pi\,r^2h$$
zu b) Kegel
Rotiere die Ursprungs-Gerade \(f(x)=\frac rh\,x\) im Intervall \(x\in[0;h]\) um die x-Achse:$$V=\int\limits_{x=0}^h\pi\left(\frac rh\,x\right)^2\,dx=\pi\,\frac{r^2}{h^2}\int\limits_{x=0}^hx^2dx=\pi\,\frac{r^2}{h^2}\left[\frac{x^3}{3}\right]_{x=0}^h=\pi\,\frac{r^2}{h^2}\cdot\frac{h^3}{3}=\frac13\pi\,r^2h$$
zu c) Kugel
Die zu rotierende Funktion \(f(x)\) ist hier nicht sofort klar. Die Idee ist, dass wir einen Viertelkreis um die x-Achse rotieren. Das liefert und das Volumen einer Halbkugel. Das Ergebnis vedoppeln wir am Ende.
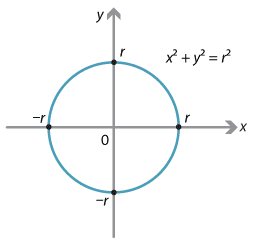
Für Punkte \((x;y)\) auf einem Kreis mit Radius \(r\) gilt nach Pythagoras:$$x^2+y^2=r^2\quad\implies\quad y^2=r^2-x^2$$Der Viertelkreis rechts oben im ersten Quadranten wird also beschrieben durch:$$f(x)=\sqrt{r^2-x^2}\quad;\quad x\in[0;r]$$Damit können wir das Integral formulieren:$$V=2\cdot\int\limits_{x=0}^r\pi(r^2-x^2)dx=2\pi\left[r^2x-\frac{x^3}{3}\right]_{x=0}^r=2\pi\left(r^3-\frac{r^3}{3}\right)=\frac43\pi\,r^3$$