Aufgabe:
Mit welcher Wahrscheinlichkeit hat die Verteilung den Wert K:
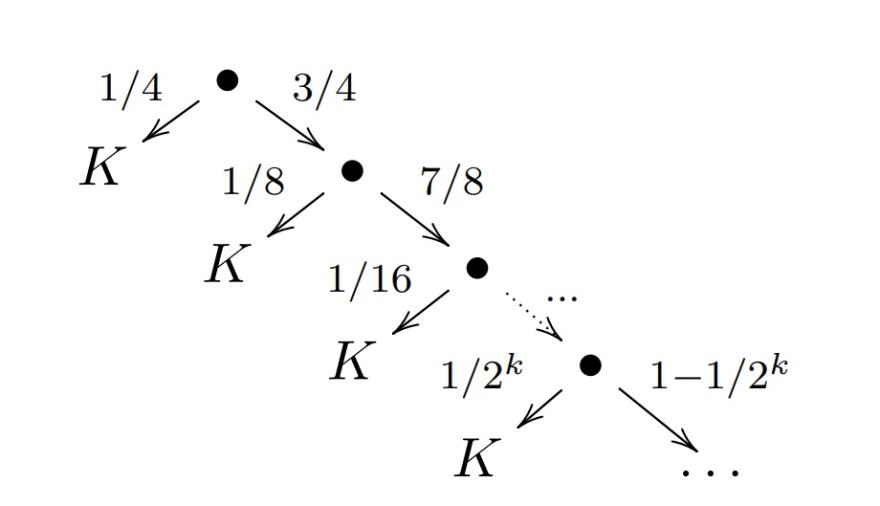
Problem/Ansatz:
In der Vorlesung heißt es, die Wahrscheinlichkeit ist exakt 5/12 ohne Begründung. Wie kommt man auf diese Lösung? Ein Ansatz von uns war es, die erwartete Lösung durch hohe Zahlen zu schätzen, jedoch stimmt die Lösung nicht:
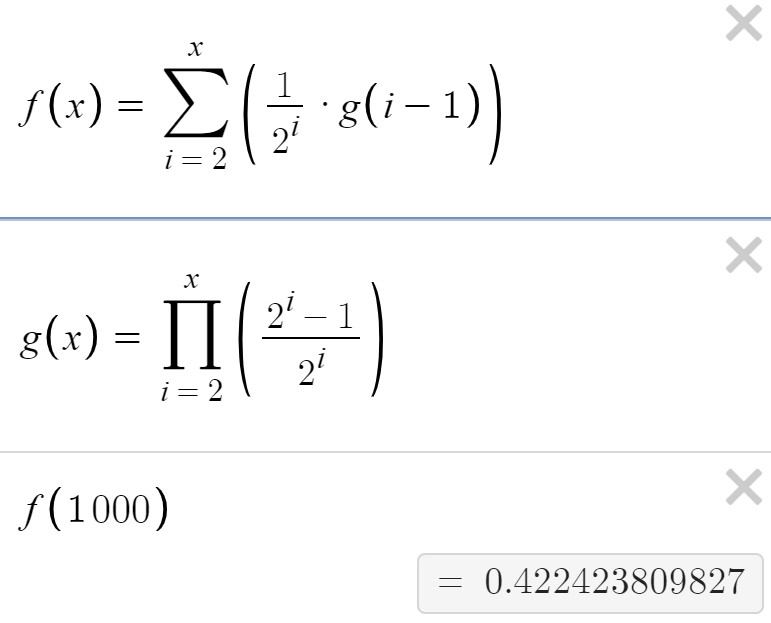
Text erkannt:
\( f(x)=\sum \limits_{i=2}^{x}\left(\frac{1}{2^{i}} \cdot g(i-1)\right) \)
\( g(x)=\prod \limits_{i=2}^{x}\left(\frac{2^{i}-1}{2^{i}}\right) \)
\( f(1000) \)
\( =0.422423809827 \)
Vielen Dank im Voraus.
LG MatheG42