Integral bei Ableitungsfunktion

Question

Aufgabe:

f(x) = x*e^(-0,5x^2+0,5)

Problem/Ansatz:

Ich habe so gerechnet:

Integral von g'(x)*e^g(x)

ist Integral von -0,5*2x*e^(-0,5x^2+0,5) Grenzen 0 und 1.

also Stammfunktion ist:

e^(-0,5x^2+0,5)

Es fehlt, was ich nicht verstehe, ein Minus davor.

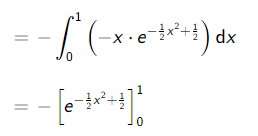
Text erkannt:

\( \begin{array}{l}=-\int \limits_{0}^{1}\left(-x \cdot e^{-\frac{1}{2} x^{2}+\frac{1}{2}}\right) d x \\ =-\left[e^{-\frac{1}{2} x^{2}+\frac{1}{2}}\right]_{0}^{1}\end{array} \)

habe das ganze ohne das Minus vor dem Integral.

Warum braucht man da ein Minus?

Comments

https://www.integralrechner.de/

Wenn du den Exponenten ableitest, erhältst du 2*(-0,5)*x = -x

Answer 1

Du sollst ja nicht

Integral von -0,5*2x*e^(-0,5x2+0,5) Grenzen 0 und 1

ausrechnen, sondern

Integral von 0,5*2x*e^(-0,5x2+0,5) Grenzen 0 und 1

Das gesuchte Integral ist daher minus "die von Dir gefundene Stammfunktion" in den Grenzen von 0 bis 1.

Comments

Woher weißt du das?

f(x) = x*e^(-0,5x2+0,5)

g'(x) * e(x)^g(x)

-> -xe^(0,5-0,5x^2)

-xe^(0,5-0,5x^2) Integral 0 bis 1

-x ist doch die Ableitung von g(x)

---

"Das gesuchte Integral ist daher minus "die von Dir gefundene Stammfunktion" in den Grenzen von 0 bis 1."

Kannst du das nochmal bitte erklären warum minus.

Ich verstehe das nicht.

---

Denke ich habe es jetzt.

Integral wäre eigentlich -x*e^(-0,5x^2+0,5) mit Grenzen 0 und 1.

Aber da die Autoren sagen, dass e^g(x) am Ende die Stammfunktion sein soll, ist e^(-0,5x^2+0,5) die Stammfunktion und nicht -x*e^(-0,5x^2+0,5).

Die Aufgabe ist für mich ungewöhnlich und fremd

---

Nein, hast du nicht verstanden.

Die Funktion selbst hat kein Minus. Durch den von dir oben genannten Grund erhält aber die Stammfunktion ein Minus.