Gleichschenkliges Trapez Flächeninhalt und Verhältnis berechnen

Question

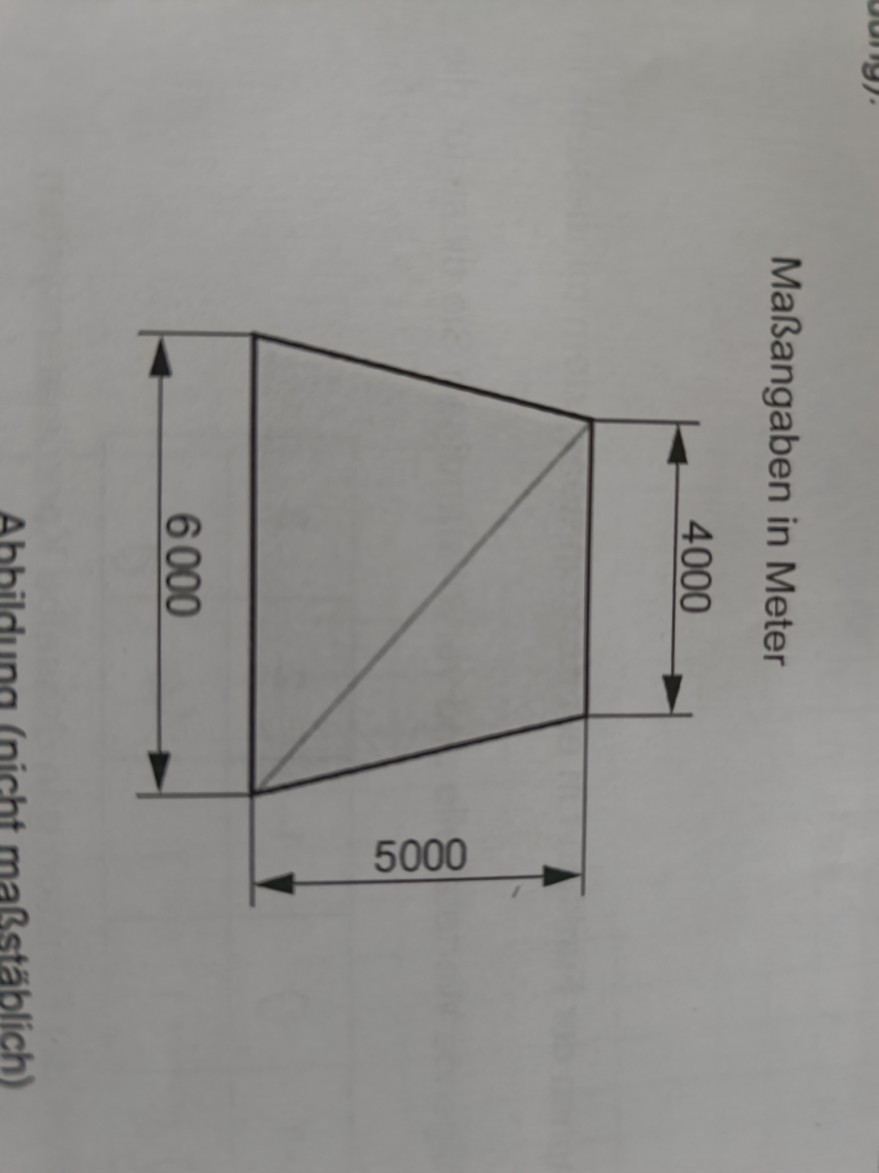
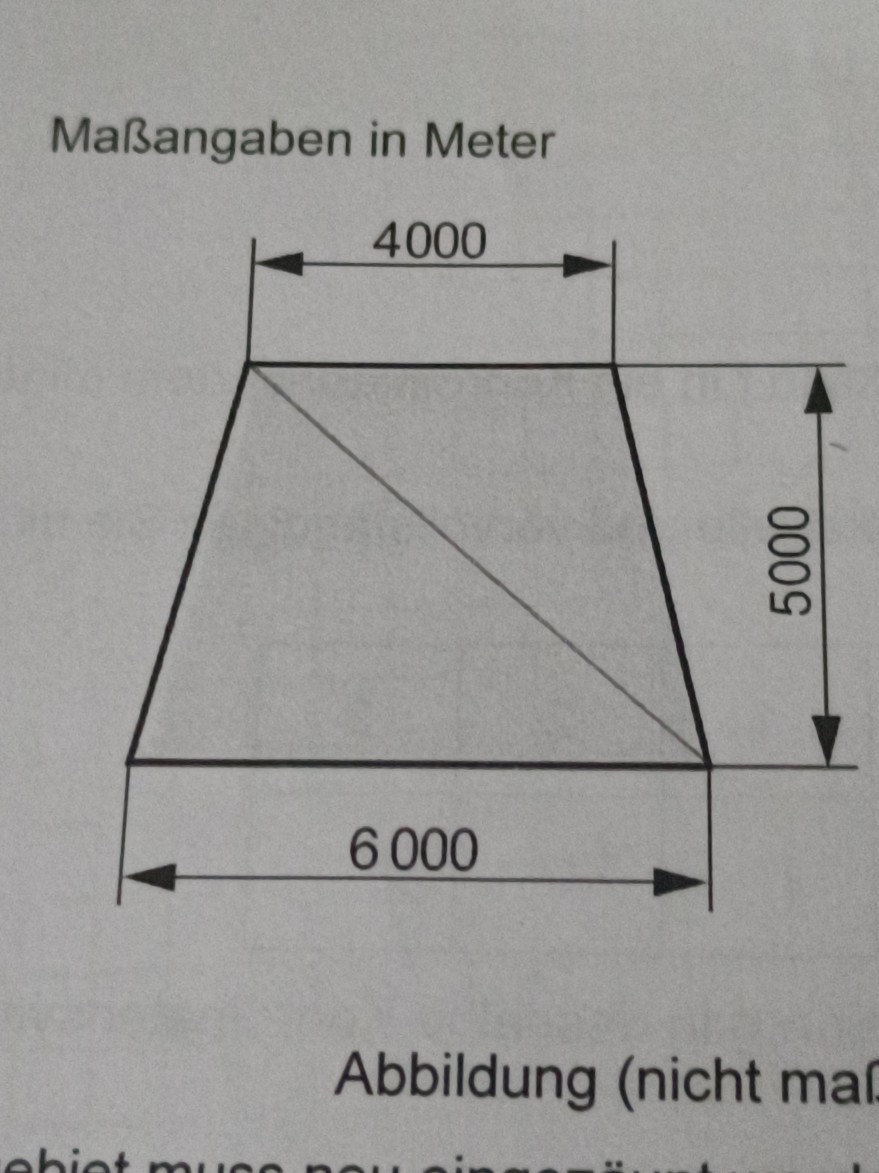
Aufgabe: Die Aufgabe lautet: Ein Weg verläuft entlang einer Diagonalen durch das Naturschutzgebiet und teilt dieses in zwei Teilflächen. Ermitteln Sie, in welchem Verhältnis der Flächeninhalt der kleineren Teilfläche zum Flächeninhalt der größeren Teilfläche steht.

Problem/Ansatz:

Hallo, ich habe für diese Aufgabe noch keinen Ansatz gefunden, trotz langem versuchen.

Text erkannt:

Maßangaben in Meter
Abbildung (nicht maf

Answer 1

Gesamtfläche:

\(A= \frac{6.000+4.000}{2}\cdot4.000=20.000.000 \)

\(A=20.000.000 m^{2} \)

Teilfläche: A,B,D

\(A_1= \frac{6.000\cdot 4.000}{2}=12.000.000 \)

\(A_1= 12.000.000m^{2} \)

\(A_2= 8.000.000m^{2} \)

Flächenverhältnis:

\( \frac{8.000.000}{12.000.000}=\frac{2}{3} \)

Comments

Warum rechnest du unnötigerweise die Inhalte der Teilflächen aus?

Answer 2

Die beiden Teildreiecke haben dieselbe Höhe. Ihre Grundseiten stehen im Verhältnis \(\frac{4000}{6000}=\frac{2}{3}\) und damit auch die Flächen, da die Fläche eines Dreiecks über \(\frac{1}{2}gh\) berechnet wird. Damit ist keine Rechnung erforderlich und auch zusätzliche Annahmen an das Trapez werden nicht benötigt.

Answer 3

Länge x der schrägen gleichlangen Seiten

x^2= √(5000^2+1000^2)

x= 5099,02

Dann die Fläche hiermit:

https://de.serlo.org/mathe/83525/fl%C3%A4cheninhalt-allgemeines-dreieck-mit-dem-sinus

Comments

Willst du den Fragesteller verarschen?

Die Dreiecke haben die gleiche Höhe. Ihre Grundseiten verhalten sich wie ...zu ...

Die Länge x ist unnötig wie ein Kropf. Wenn du noch dazu einen Näherungswert dafür verwendest, kann der Fragesteller kaum auf das richtige ganzzahlige Verhältnis kommen.

---

Ich möchte ihn ein wenig rechnen lassen.

Beschäftigungstherapie wie in vielen Unterrichtsstunden.

---

Eine sehr schwache Ausrede.

---

x²= √(5000²+1000²)
Erstens wird im Aufgabentext zwar nicht gesagt, dass das Naturschutzgebiet trapezförmig ist (was man aber wohl annehmen kann), aber dass es sich dabei um ein gleichchenkliges Trapez handelt, wird erst recht nicht gesagt - uns das muss man auch nicht annehmen.
Zweitens ist die Gleichung sowieso falsch.

das richtige ganzzahlige Verhältnis
Willst du den Fragesteller .. in die Irre führen ?