Vektoren Koordinaten berechnen

Question

Aufgabe: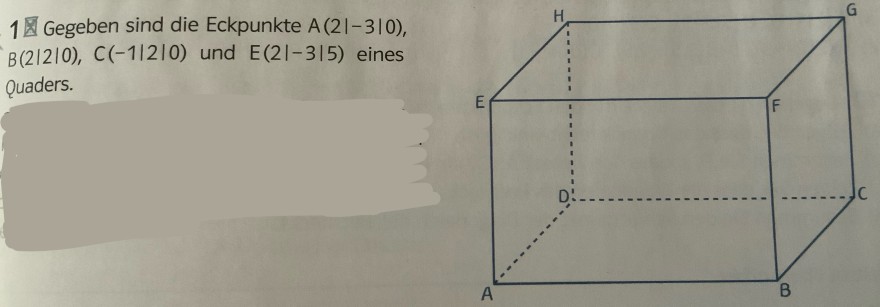

Text erkannt:

1图 Gegeben sind die Eckpunkte \( A(2|-3| 0) \), \( B(2|2| 0), C(-1|2| 0) \) und \( E(2|-3| 5) \) eines Quaders.

Problem/Ansatz:

Ich habe diese Aufgabe gelöst und sie im Internet gefunden. Ich sehe aber immer, dass der Punkt D die Koordinaten (-1 | -3 | 0) hat. Ich habe aber (-1 | -3 | 10) raus.

Meine Rechnung:

1. \( \vec{AE} \) = \( \begin{pmatrix} 2\\-3\\ 5 \end{pmatrix} \) - \( \begin{pmatrix} 2\\-3\\0 \end{pmatrix} \) = \( \begin{pmatrix} 0\\0\\5 \end{pmatrix} \)

2. \( \vec{AE} \) + \( \vec{OH} \) =  \( \begin{pmatrix} 0-1\\0-3\\ 5+5 \end{pmatrix} \) =  \( \begin{pmatrix} -1\\-3\\ 10 \end{pmatrix} \)

Kann mir es jemand korrigieren?

Answer 1

Ich weiß nicht, was Du da rechnest. Der Nullpunkt ist ja im Bild gar nicht eingetragen.

Zur Berechnung von D brauchst Du nur die Bodenebene betrachten mit A, B, C.

Comments

Nachdem man alle anderen Punkte berechnet hat, kann man die auch benutzen. Ich habe H berechnet und dann kann ich ja den Vektor von AE einfach zu OH addieren, weil es die selbe Länge hat. Aber trotzdem danke!

---

Nein, es geht eben 1. nicht um Längen und 2. ist der Nullpunkt nicht im Bild.

Es geht um Vektoren, die addiert man durch Aneinanderhängen. Und es ist immer sicherer, direkt mit den Angaben aus der Aufgabenstellung zu arbeiten als mit selbst berechneten (Zwischen-)Ergebnissen.

Answer 2

Wenn du den Vektor \(\overrightarrow{AE}\) zu \(\overrightarrow{OH}\) addierst, dann landest du ja oberhalb von \(H\). Du gehst also in die falsche Richtung. Du musst \(\overrightarrow{AE}\) von \(\overrightarrow{OH}\) subtrahieren, damit du in die richtige Richtung gehst und dann kommt auch das richtige heraus. Prüfe das nochmal nach.

Comments

Jetzt habe ich es verstanden. Wirklich danke!!

---

Das ist prima.

Answer 3

Bei den gegebenen Koordinaten kann man von A oder von C nach D gehen:

\( \overrightarrow{OD} = \overrightarrow{OA} + \overrightarrow{BC} = \begin{pmatrix} 2\\-3\\0 \end{pmatrix} + \begin{pmatrix} -1-2\\2-2\\0-0 \end{pmatrix} = \begin{pmatrix} -1\\-3\\0 \end{pmatrix} \)

\( \overrightarrow{OD} = \overrightarrow{OC} + \overrightarrow{BA} = \begin{pmatrix} -1\\2\\0 \end{pmatrix} +\begin{pmatrix} 2-2\\-3-2\\0-0 \end{pmatrix} = \begin{pmatrix} -1\\-3\\0 \end{pmatrix} \)