Hallo Sophia,
… Ich weiß nicht, wie der Abstand von 9LE mir bei der Ermittlung der Koordinaten helfen soll.
mache Dir ein Bild von der Aufgabe
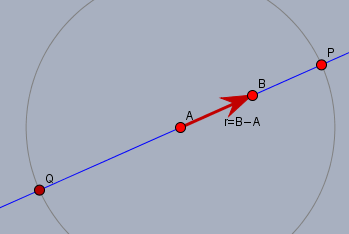
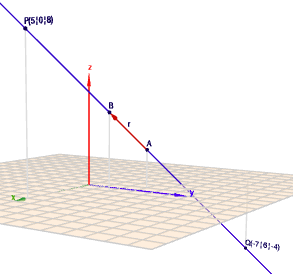
\(P\) und \(Q\) liegen auf der Geraden \(g\) (oben blau) und haben vom Punkt \(A\) den Abstand \(9\). Wenn man jetzt weiß wie lang der Vektor \(\vec{r}=B-A\) ist, dann könnte man doch diesen Vektor so verlängern (oder verkürzen), dass er die Länge \(9\) hat. Und dann addiert und subtrahiert man den in der Länge veränderten Vektor zu \(A\) und kommt zu \(P\) und \(Q\)
Weißt Du wie man die Länge von \(\vec{r}=B-A\) berechnet?
....
zur Kontrolle kannst Du die Ergebnisse von \(P\) und \(Q\) unten ablesen. Wenn Du auf das Bild klickst, siehst Du es besser