Ermittlung von Punkten auf einem Kreisbogen, der Kreis ausschließlich im ersten Quadranten liegt.

Question

Aufgabe: Ich möchte Punkte auf dem Kreisbogen berechnen, wenn der Kreis ausschließlich im ersten Quadranten liegt. Also auch der Mittelpunkt etc.

Problem/Ansatz: Normalerweise, wenn der Kreis seinen Mittelpunkt im Ursprung hat, dann sind die Koordinaten (cos(alpha)/ sin(alpha)). Hier ist dies aber ausgeschlossen.

Ich habe gegeben: Den Mittelpunkt M, den Radius R, und den Winkel Alpha1...Alpha5 je nachdem wo der Punkt auf dem Kreisbogen liegen soll.

Jetzt weiß ich aber nicht genau wie ich daraus eine Formel entwickel.

Ich hoffe jemand kann mit diesen Bescheidenen Informationen schon was anfangen ohne zu sehr in die Tiefe zu gehen.

Mit freundlichen Gruß

Answer 1

Hier die Skizze

Gegeben
M ( mx | my )
r = radius

Allgemeine Kreisgleichung

r^2 = ( x - mx ) ^2 + ( y -my )^2

Was ist jetzt dein Begehr ?

aus x wird y
Vom Koordinatenursprung
tan ( alpha ) = y / x

Comments

Ich hab noch die Parameterschreibweise gefunden x = xm + radius * cos(winkel), y = ym + radius * sinus(winkel) Damit klappts denke auch. Danke euch

Answer 2

Schneide z.B. den Kreis (x-4)^2+(y-4)^2 =9 mit der Ursprungsgeraden y=m*x

Dann kannst du die jeweiligen Koordinaten der Schnittpunkte berechnen.

mfG

Moliets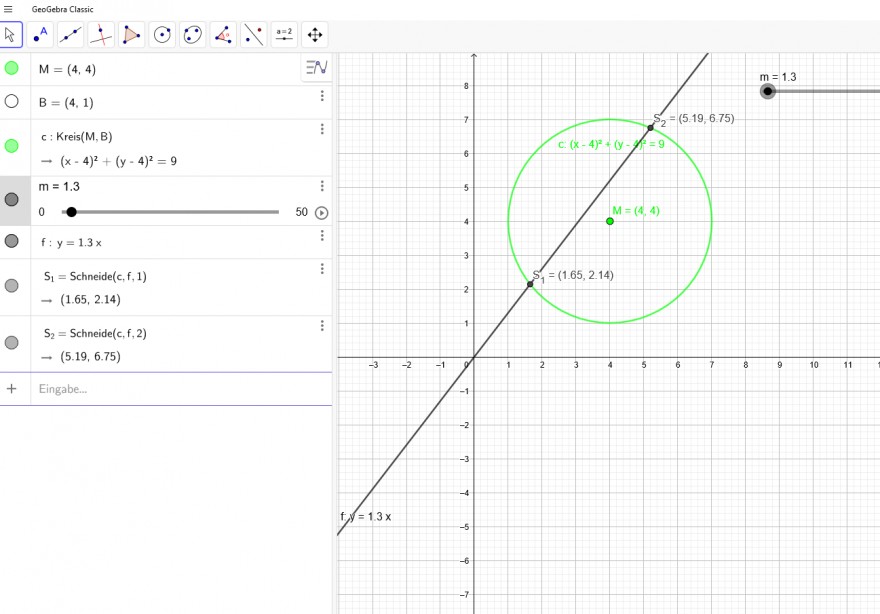

Text erkannt:

\( \mathrm{M}=(4,4) \)
\( B=(4,1) \)
c: \( \mathrm{Krelis}(\mathrm{M}, \mathrm{B}) \)
\( -(x-4)^{2}+(y-4)^{2}=9 \)
\( \mathrm{S}_{1}=\mathrm{Schneide}(\mathrm{c}, \mathrm{f}, 1) \)
\( -(1.65,2.14) \)
\( \mathrm{s}_{2}= \) Schneide \( (c, \mathrm{f}, 2) \)
\( -(5.19,6 \)

Comments

Hi, coole Idee ich hab aber die Steigung der Geraden leider nicht.

Ich hab nur den Winkel und den Radius und Mittelpunkt. Ich kann leider kein Bild einfügen deswegen Schematisch.

Wenn das der Kreis ist in klein dann sind es in diesem Fall vier Winkel am Mittelpunkt liegend und die habe ich.
⊗


und Danke für die Antwort schonmal

---

Doch er hat es, also der Winkel zwischen e und v zum Beispiel habe ich oder zwischen v und u etc. + Mittelpunkt und Radius

---

M(4 |4) ; r=3  und α=30°     Geradengleichung: \( \frac{y-4}{x-4} \) =tan 30°

tan(30°)=...

Diese Gleichung nun nach y auflösen und mit dem Kreis schneiden, ergibt die beiden Schnittpunkte.

mfG

Moliets

M

---

Super vielen dank werde es gleich mal ausprobieren. Nur interessehalber würde dir ein weg über die Winkelfunktionen einfallen?