Aufgabe:
In einem kartesischen Koordinatensystem ist der Körper ABCDPQRS mit \( A(28|0| 0), B(28|10| 0), C(0|10| 0), D(0|0| 0) \) und \( P(20|0| 6) \) gegeben. Der Körper ist ein schiefes Prisma, die Grundfläche \( A B C D \), die Deckfläche PQRS und die vier Seitenflächen sind also Parallelogramme.
a) Zeigen Sie, dass die Seitenfläche ABQP quadratisch ist.
b) Stellen Sie das Prisma in einem Koordinatensystem grafisch dar.
c) Die Seitenfläche ABQP liegt in einer Ebene E. Ermitteln Sie eine Gleichung von E in Koordinatenform. \( \text { (zur Kontrolle: } E: 3 x+4 z-84=0 \text { ) } \)
d) Die Seitenfläche CDSR liegt in einer Ebene F. Begründen Sie ohne zu rechnen, dass \( F \) durch die Gleichung \( 3 x+4 z=0 \) beschrieben werden kann.
Durchmesser wird im Modell vernachlässigt.
e) Bestimmen Sie im Modell die Koordinaten des Punkts, in dem die Stange in der Bohrung endet.
Das Prisma beschreibt modellhaft den Grundkörper eines Kunstwerks aus massivem Beton, der auf einer horizontalen Fläche steht. Eine Längeneinheit im Koordinatensystem entspricht \( 0,1 \mathrm{~m} \) in der Wirklichkeit.
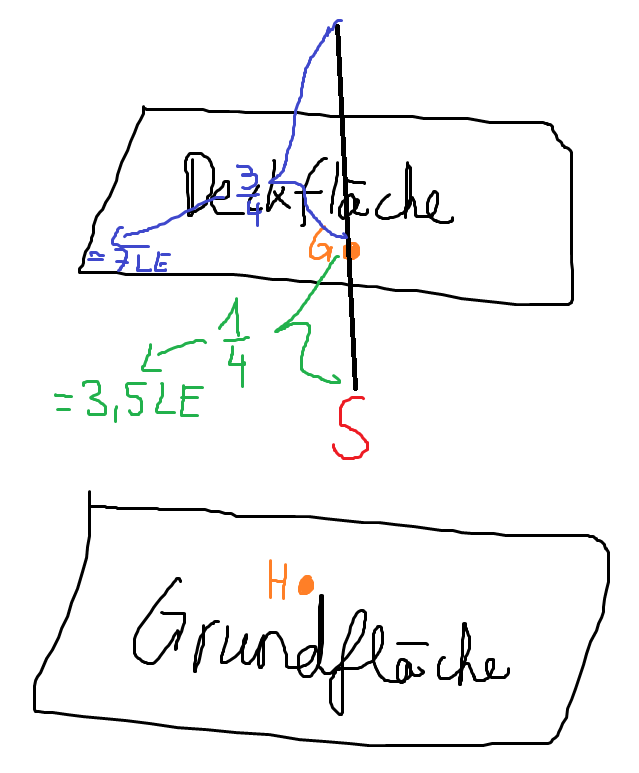
Der Grundkörper ist mit einer dünnen geradlinigen Bohrung versehen, die im Modell vom Punkt G(11|3|6) der Deckfläche aus in Richtung des Schnittpunkts der Diagonalen der Grundfläche verläuft. In der Bohrung ist eine gerade Stahlstange mit einer Länge von \( 1,4 \mathrm{~m} \) so befestigt, dass die Stange zu drei Vierteln ihrer Länge aus der Deckfläche herausragt und in einer Höhe von \( 0,9 \mathrm{~m} \) über der Deckfläche endet. Ihr
Ich habe eine Frage zur e)
Quelle: https://www.iqb.hu-berlin.de/abitur/sammlung/abitur/sammlung/mathematik/erhoeht/Beispielaufgaben_15.pdf
Problem/Ansatz:
Dies ist meine Skizze und ich verstehe die Lösung.
Allerdings habe wollte ich rechnen:
OS = OG + 3.5 * GH
und das ist falsch..
Warum darf ich die 3.5 LE die ich berechnet habe aus 1/4 * 1,4m nicht als Geradenparameter nutzen?
Ich gehe doch von G 3.5LE Richtung GH.. und bei 3.5LE von G runter.. wäre ich bei S (Bohrungsende)