Question

Funktionenschaar untersuchen auf Extrempunkte:

\( f a(x)=\frac{-3}{4 t^{2}} x^{4}+\frac{5}{4 t^{2}} x^{3}+2 t \)

Meine Ableitungen:

fa'(x)=-3t²x³+3,75t²x²

fa''(x)=-9t²x²+7,5t²x

x1=0 x2= 1,25

Wo ich ein Problem habe ist das einsetzen der zweiten nullstelle 1,25 in die 2. Ableitung, um zu sehen ob es ein Hoch- oder Tiefpunkt ist. Laut lösung kommt -75/16t² raus.

Answer 1

f_a(x) = -3/(4t²) * x⁴ + 5/(4t²) * x³ + 2t

Erstaunlich, dass auf der rechten Seite kein a vorkommt :-)

f'_a(x) = -3*4/(4t²) * x³ + 5*3/(4t²) * x² = -3/t² * x³ + 15/(4t²) * x²

f''_a(x) = -9/t² * x² + 15/(2t²) * x

Eine (doppelte) Nullstelle der ersten Ableitung ist x₁ = 0, wie man leicht herausfindet, indem man x² ausklammert:

f'_a(x) = x² * [-3/t² * x + 15/(4t²)]

Setzen wir den 2. Faktor gleich 0, um die zweite Nullstelle zu finden:

15/(4t²) = 3/t² * x | : 3/t²

x₂ = 15/(4t²) * t²/3 = 5/4 = 1,25

Wir setzen x₁ und x₂ in die 2. Ableitung ein:

f''_a(0) = 0 => kein Extremum an der Stelle x₁ = 0

f''_a(1,25) = -9/t² * 1,5625 + 15/(2t²) * 1,25 | Erweitern mit 2

f''_a(1,25) = -18/(2t²) * 1,5625 + 15/(2t²) * 1,25 = -28,125/(2t²) + 18,75/(2t²) < 0, da 2t² für jedes t positiv

=> Maximum an der Stelle x₂ = 1,25

1,25 muss man dann in die Ursprungsfunktion einsetzen, um den entsprechenden Funktionswert zu bestimmen - mache ich nachher in einem Kommentar, falls mir niemand zuvorgekommen ist :-)

Nun setzen wir, wie versprochen, noch 1,25 in die Ursprungsfunktion ein:

f_a(1,25) = -3/(4t²) * 2,44140625 + 5/(4t²) * 1,953125 + 2t =

-7,32421875/(4t²) + 9,765625/(4t²) + 2t =

2,44140625/(4t²) + 2t

Nicht gerade ein sehr schönes Ergebnis :-)

Eine "normale" Dezimalzahl wird man bei Aufgaben dieser Art nicht bekommen, da es ja gerade der Witz von Funktionenscharen ist, dass sie von dem f-Index abhängen. Deshalb vermute ich auch, dass die Funktion eigentlich lauten soll:

f_t(x) = -3/(4t²) * x⁴ + 5/(4t²) * x³ + 2t

Nehmen wir einmal t = 1 und ein zweites Mal t = 2, dann ergeben sich folgende Graphen:

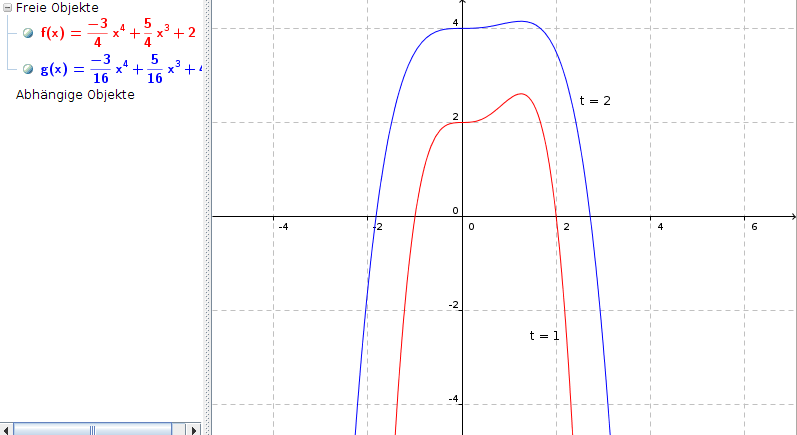
Man sieht, dass in beiden Fällen ein Maximum bei x = 1,25 vorliegt, aber die entsprechenden y-Werte (Funktions-Werte) sind natürlich - abhängig von t - sehr unterschiedlich!

Besten Gruß

Answer 2

In der ersten Ableitung ist schon falsch abgeleitet worden sein.

fa ´ ( x ) = 3 / t^2 * x^3  + 3.75 / t^2* x^2
fa ´( x ) = x^2 * ( 3 / t^2 * x  + 3.75 / t^2)
ein Produkt ist dann null wenn mindestens einer der Faktoren null ist.
x = 0
3  / t^2 * x + 3.75 / t^2 = 0
3 / t^2 * x = - 3.75 / t^2
x = - 3.75 / 3
x = - 1.25

2.Ableitung
fa ´´ ( x ) = 9 / t^2 * x^2 + 7.5 / t^2 * x
fa ´´ ( 0 ) = 0  | dürfte ein Sattelpunkt sein
fa ´´ ( -1.25 ) = 9 / t^2 * (-1.25)^2 + 7.5 / t^2 * ( -1.25 )
fa´´ ( -1.25 ) = 14.0625 / t^2 - 9.375 / t^2
fa ´´ ( -1.25 ) = 4.6875 / t^2 = -75/(16 *t^2)

t^2 ist immer positiv. -75/(16 *t^2) ist negativ.  Also ein Hochpunkt.

Bei Fehlern oder Fragen wieder melden.

mfg Georg

Nachtrag : selbst einen Fehler gemacht. Der erste Summand
muß negativ sein. Korrigiere aber nichts mehr.