Ist hier die Formel E[X^2] = x^2 * p(x) anzuwenden?

Question

Aufgabe:

Ist hier die Formel E[X^2] = x^2 * p(x) anzuwenden?

Problem/Ansatz:

Also ist mein Rechenweg bei Nummer iii) so richtig?

Text erkannt:

(a) Sei \( p_{c} \) die Funktion auf \( \{0, \ldots, 4\} \) mit
\( p_{c}(0)=c, \quad p_{c}(1)=\frac{1}{4}, \quad p_{c}(2)=\frac{3}{16}, \quad p_{c}(3)=\frac{1}{8}, \quad p_{c}(4)=\frac{1}{16}, \)
wobei \( c \in \mathbb{R} \) ein Parameter ist.
(i) Für welches \( c \) ist \( p_{c} \) eine Wahrscheinlichkeitsfunktion?
(2 Punkte)

Sei nun \( X \) eine diskrete Zufallsvariable mit \( P(X=x)=p_{c}(x) \) für alle \( x \), wobei \( c \) der Parameter aus (i) ist.
(ii) Berechnen Sie \( P(|X-2| \leq 1) \).
(3 Punkte)
(iii) Bestimmen Sie \( E\left[X^{2}\right] \).
(2 Punkte)

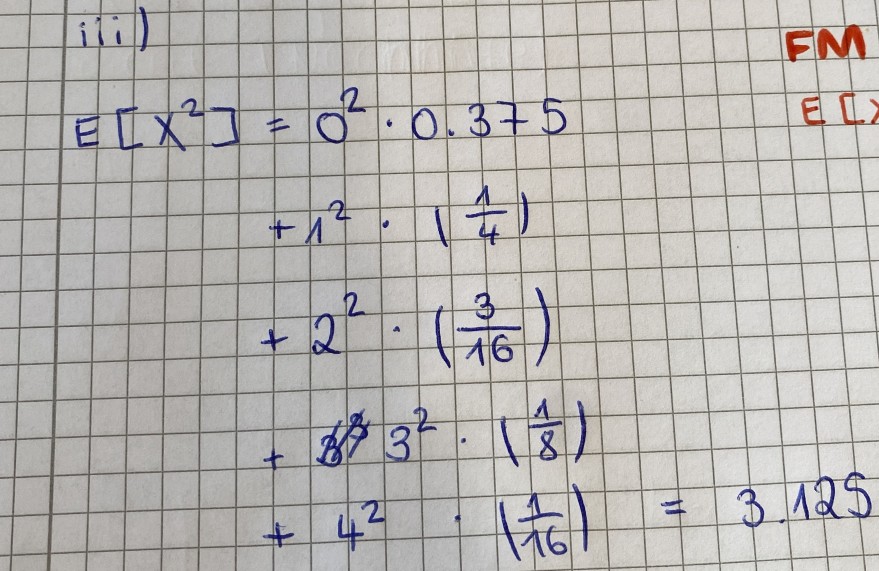
Text erkannt:

\( \begin{aligned} E\left[X^{2}\right] & =0^{2} \cdot 0.375 \\ & +1^{2} \cdot\left(\frac{1}{4}\right) \\ & +2^{2} \cdot\left(\frac{3}{16}\right) \\ & +3^{2} \cdot\left(\frac{1}{8}\right) \\ & +4^{2} \cdot\left(\frac{1}{16}\right)=3.125\end{aligned} \)

Answer 1

Deine Rechnung war richtig

E(X²) = 0^2·3/8 + 1^2·1/4 + 2^2·3/16 + 3^2·1/8 + 4^2·1/16 = 25/8 = 3.125

Die Formel

E(X²) = x^2·p(x)

ist aber so verkehrt. Wo bleibt denn auf der rechten Seite z.B. die Summe?