Aufgabe:
Integriere mit der Substitutionsregel
Text erkannt:
\( \int \frac{1}{\sqrt{1-x^{2}}} d x \)
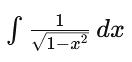
Problem/Ansatz:
Was ist das für ein Schwachsinn. Ich muss diesen Formelsalat hier einfügen, anstatt das Bild hochzuladen.
Das wird doch viel unverständlicher für die lieben Beantworter sein. Naja, dann halt schriftlich :
Mein Prof. hat hier x(t) mit sin(t) substituiert und danach für die Wurzel aus (1 - sin^2(t)) → cos(t) eingesetzt.
Außerdem hat er die Ableitung von x(t) berechnet (also cos(t)) und mit dx/dt gleichgesetzt. Vorher haben wir immer dt/dx gerechnet. Außerdem sind die Intervallgrenzen von 0 bis 1 zu arcsin(0) bis arcsin(1) geworden.
Ich verstehe nun nicht wieso er einfach sin durch x eintauschen kann und wieso die Intervallgrenzen so sind wie sie sind. Laut definition müssten sie doch die Ableitung von unserer Substitution sein oder verstehe ich hier etwas falsch?
Vielen Dank für jede Hilfe!!!