DGL und Defintionsintervalle

Question

Aufgabe:

Lösen Sie die reelle DGL y^3*y' - (1/2)*t^-1 = -1/(4*t) mit dem AWP y(-1) = -2 und bestimmen sie das maximale Definitionsintervall, auf dem die Lösung definiert ist.

Problem/Ansatz:

Hi, ich habe Probleme mit dieser Aufgabe weiterzukommen, besonders bei dem y^3 und dem t^-1. Falls jemand eine detaillierte Lösung mit Schritten hätte wäre ich sehr dankbar dafür! :)

Comments

Ich finde es etwas merkwürdig, dass in der DGL 1/(4t) als (1/(2t)-1/(4t) notiert wird. Ist das die Originalaufgabe?

Answer 1

Hallo,

Lösung via Trennung der Variablen:

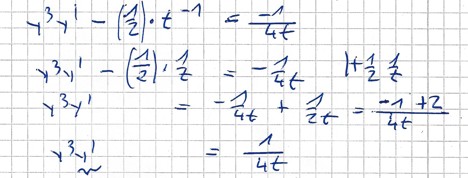
Man kann noch 4c= C₁ setzen

Dann die AWB y(-1) = -2 in die Lösung einsetzen:

die positive Lsg . entfällt wegen der AWB:

Lösung:

\( y=-\sqrt[4]{\ln |t|+16} \)

maximales Definitionsintervall:

\( \left\{x \in \mathbb{R}: x \leq-\frac{1}{e^{16}}\right. \) oder \( \left.x \geq \frac{1}{e^{16}}\right\} \)