Text erkannt:
2. Was ist \( \mathbb{E}(\alpha X) \) ?

Text erkannt:
Gegeben sei \( \Omega \subseteq \mathbb{R} \) und eine stetige reelle Zufallsvariable \( X: \Omega \rightarrow \mathbb{R} \) mit pdf \( p: \mathbb{R} \rightarrow[0, \infty) \) und zwei reelle Zahlen \( \alpha \neq 0, \beta \in \mathbb{R} \). Wir nehmen an, dass \( \mu:=\mathbb{E} X \) und \( \sigma^{2}:=\mathbb{V} X \) existieren. Sei \( Y:=\frac{X-\beta}{\alpha} \).
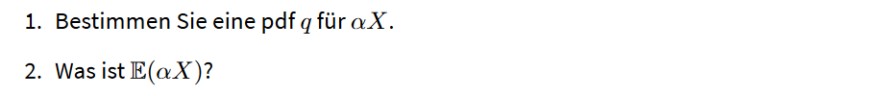
Text erkannt:
1. Bestimmen Sie eine pdf \( q \) für \( \alpha X \).
2. Was ist \( \mathbb{E}(\alpha X) \) ?

Text erkannt:
Tipp: Für eine Funktion \( g: \mathbb{R} \rightarrow \mathbb{R} \) gilt \( P(g(X) \in A)=P\left(X \in g^{-1}(A)\right) \) für jede Menge \( A \subseteq \mathbb{R} \). Eine nützliche solche Funktion \( g \) könnte z.B. \( x \mapsto \alpha x \) sein, oder \( x \mapsto x-\beta \).
Tipp 2: Die Transformationsformel für Integrale besagt für Funktionen \( f, g: \mathbb{R} \rightarrow \mathbb{R} \) (wobei \( g \) differenzierbar ist), dass
\( \int \limits_{g(A)} f(x) d x=\int \limits_{A} f(g(x))\left|g^{\prime}(x)\right| d x . \)
Das dürfen Sie ohne Beweis benutzen.
Text erkannt:
Tipp 2: Die Transformationsformel für Integrale besagt für Funktionen \( f, g: \mathbb{R} \rightarrow \mathbb{R} \) (wobei \( g \) differenzierbar ist), dass
\( \int \limits_{g(A)} f(x) d x=\int \limits_{A} f(g(x))\left|g^{\prime}(x)\right| d x . \)
Das dürfen Sie ohne Beweis benutzen.
Text erkannt:
Tipp 2: Die Transformationsformel für Integrale besagt für Funktionen \( f, g: \mathbb{R} \rightarrow \mathbb{R} \) (wobei \( g \) differenzierbar ist), dass
\( \int \limits_{g(A)} f(x) d x=\int \limits_{A} f(g(x))\left|g^{\prime}(x)\right| d x . \)
Das dürfen Sie ohne Beweis benutzen
Text erkannt:
2. Was ist \( \mathbb{E}(\alpha X) \)
Problem/Ansatz:
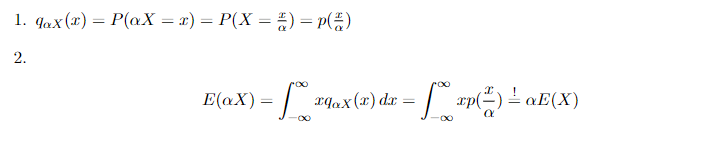
Text erkannt:
1. \( q_{\alpha X}(x)=P(\alpha X=x)=P\left(X=\frac{x}{\alpha}\right)=p\left(\frac{x}{\alpha}\right) \)
2.
\( E(\alpha X)=\int \limits_{-\infty}^{\infty} x q_{\alpha X}(x) d x=\int \limits_{-\infty}^{\infty} x p\left(\frac{x}{\alpha}\right) \stackrel{!}{=} \alpha E(X) \)
Ab 2. komme ich nicht mehr weiter. Ich denke das Ziel ist es am Ende E(αX) = αE(X) zu zeigen.
Außerdem nehme ich an, dass man die Transformationsformel braucht um über |g'(x)| α aus dem Integral zu ziehen.
Allerdings ist mir nicht klar, wie ich die Formel hier korrekt anwende.